
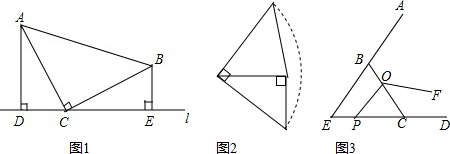
分析 (1)由同角的余角相等,和直角判断出△ADC≌△CEB;
(2)由旋转得到结论,判断出四边形C′ADB′是矩形,再用面积公式计算即可;
(3)由等式的性质判断出∠BFO=∠CPO,从而得到△OCP≌△FBO,求出CP,即可.
解答 证明:(1)∵∠DAC+∠DCA=∠ECB+∠DCA=90°,
∴∠DAC=∠ECB,
在△ADC和△CEB中,
$\left\{\begin{array}{l}{∠ADC=∠CEB}\\{∠DAC=∠ECB}\\{AC=CB}\end{array}\right.$
∴△ADC≌△CEB;
(2)如图1,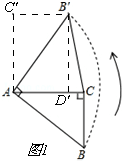
根据题意得出旋转后图形,AC′⊥AC,B′D′⊥AC,
∵∠C′AC=∠AC′B′=∠AD′B′,
∴四边形C′AD′B′是矩形,
∴AC′=B′D′=AC=4,
∴S△AB′C=$\frac{1}{2}$AC×B′D′=$\frac{1}{2}$×4×4=8;
(3)如图2,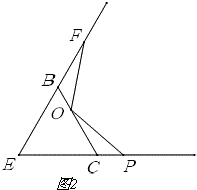
∵△BCE是等边三角形,
∴∠CBE=∠BCE=60°,
∴∠OBF=∠OCP=120°,
∴∠BOF+∠BFO=60°,
∵∠POF=120°,
∴∠BOF+∠OPC=60°,
∴∠BFO=∠CPO,
∵OP=OF,
∴△OCP≌△FBO,
∴CP=BO=BC-OC=3-2=1,
∴EP=EC+CP=3+1=4,
∵动点P从点E沿射线EC以1cm/s速度运动,
∴t=4÷1=4s.
点评 此题是几何变换综合题,主要考查了三角形的全等的判定和性质,矩形的判定和性质,等式的性质,三角形的面积公式,利用等式的性质判断∠BFO=∠CPO是解本题的难点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
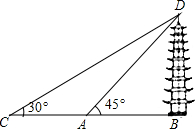 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
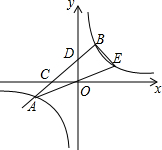 如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.
如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
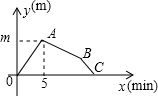 哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.
哥哥和弟弟同时从家沿同一条路去同一所学校上学,弟弟步行,哥哥骑自行车,两人都匀速前进.弟弟步行每分钟走60米,哥哥骑自行车每分钟行驶160米.如图是两人之间的距离y与弟弟步行时间x之间的函数图象.请解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
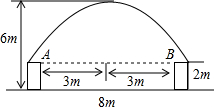 某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)
某一隧道内设双行线公路,其截面由一长方形和一抛物线构成,如图所示,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m,若行车道总宽度AB为6m,请计算车辆经过隧道时的限制高度是多少米?(精确到0.1m)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
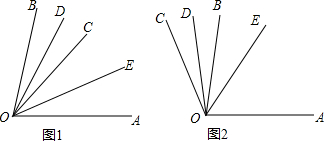 已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.
已知:∠AOB=80°,OD、OE分别是∠BOC和∠COA的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com