
【题目】已知A=x-2y,B=-x-4y+1.
(1)求2(A+B)-(A-B);(结果用含x,y的代数式表示)
(2)当![]() 与
与![]() 互为相反数时,求(1)中代数式的值.
互为相反数时,求(1)中代数式的值.
科目:初中数学 来源: 题型:
【题目】如图,已知点O为直线AB上一点,将一直角三角板的直角顶点放在点O处.
(1)如图1,将三角板的一边ON与射线OB重合,过点O在三角板的内部,作射线OC,使∠NOC:∠MOC=2:1,求∠AOC的度数;
(2)如图2,将三角板绕点O逆时针旋转一定角度到图2的位置,过点O在三角板MON的内部作射线OC,使得OC恰好是∠MOB对的角平分线,此时∠AOM与∠NOC满足怎样的数量关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】读题画图计算并作答
画线段AB=3 cm,在线段AB上取一点K,使AK=BK,在线段AB的延长线上取一点C,使AC=3BC,在线段BA的延长线取一点D,使AD=![]() AB.
AB.
(1)求线段BC、DC的长?
(2)点K是哪些线段的中点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为完善人口发展战略,我国现已全面提倡实施一对夫妇可生育两个孩子的政策.某中学为了解在校生对父母再生“二胎”的同意情况,在校园内随机调查了部分学生对“二胎”的同意情况(把调查的结果分为四个等级:A非常同意;B:同意;C:无所谓;D:坚决反对),并将调查结果绘成了如下两幅不完整的统计图. 请根据统计图中的信息解答下列问题:
(1)本次被抽样调查的学生有多少人?
(2)将两幅统计图补充完整:
(3)若全校共有3600名学生,估计“非常同意“父母再生“二胎”的大约有多少人?
(4)若从3名“同意”父母生“二胎”和2名“坚决反对”父母生“二胎”的学生中随机抽取两名学生,用树状图或列表法求抽取的两个恰好都“坚决反对”父母生“二胎”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为-20,点B表示的数为16.动点P从点A出发,以每秒6个单位长度的速度沿数轴向右匀速运动,动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动.若点P、Q同时出发,设运动时间为t(t>0)秒.
(1)填空:①点A、B之间的距离为 ;
②点P表示的数为 ,点Q表示的数为 (用含t的代数式表示);
(2)当点P、Q到原点O的距离相等时,求t的值并求出此时点Q表示的数;
(3)若点P从点A出发到达点B后立刻返回到点A并保持速度不变,点Q到达点A时停止运动,问点P运动多少秒时与点Q相距6个单位长度?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列变形中:
①由方程![]() =2去分母,得x﹣12=10;
=2去分母,得x﹣12=10;
②由方程![]() x=
x=![]() 两边同除以
两边同除以![]() ,得x=1;
,得x=1;
③由方程6x﹣4=x+4移项,得7x=0;
④由方程2﹣![]() 两边同乘以6,得12﹣x﹣5=3(x+3).
两边同乘以6,得12﹣x﹣5=3(x+3).
错误变形的个数是( )个.
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
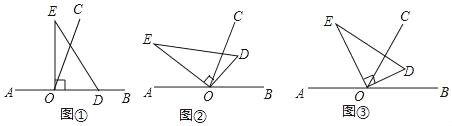
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角形的直角顶点放在点O处.(注:∠DOE=90°)
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O逆时针方向转动到某个位置,若OC恰好平分∠BOE,求∠COD的度数;
(3)如图③,将直角三角板DOE绕点O转动,如果OD始终在∠BOC的内部,试猜想∠BOD和∠COE有怎样的数量关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读材料)
平面直角坐标系中,点P(x,y)的横坐标x的绝对值表示为|x|,纵坐标y的绝对值表示为|y|,我们把点P(x,y)的横坐标与纵坐标的绝对值之和叫做点P(x,y)的勾股值,记为[P],即[P]=|x|+|y|(其中的“+“是四则运算中的加法),例如点P(1,2)的勾股值[P]=|1|+|2|=3.
(解决问题)
(1)求点A(-2.4),B(![]() +
+![]() -
-![]() )的勾股值[A],[B];
)的勾股值[A],[B];
(2)若点M在x轴的上方,其横,纵坐标均为整数,且[M]=3,请直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,∠BAC=36°,将△ABC绕点A按逆时针旋转角度ɑ(0°<ɑ<180°)得到△ADE,连接CE、BD,BD与CE相交于点F。
(1)求证:BD=CE
(2)当ɑ等于多少度时,四边形AFDE是平行四边形?并说明理由。


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com