
 如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.
如图,点C在线段AB上,AC=12厘米,CB=8厘米,点M、N分别是AC、BC的中点.分析 (1)根据“点M、N分别是AC、BC的中点”,先求出MC、CN的长度,再利用MN=CM+CN即可求出MN的长度;
(2)与(1)同理,先用AC、BC表示出MC、CN,MN的长度就等于AC与BC长度和的一半;
(3)根据中点定义可得:AM=MC=$\frac{1}{2}$AC,CN=BN=$\frac{1}{2}$CB,再根据线段之间的和差关系进行转化即可.
解答 解:(1)∵点M、N分别是AC、BC的中点,
∴CM=$\frac{1}{2}$AC=6cm,CN=$\frac{1}{2}$BC=4cm,
∴MN=CM+CN=6+4=10cm;
(2)MN=$\frac{1}{2}$a(cm),
理由如下:
同(1)可得CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CM+CN=$\frac{1}{2}$AC+$\frac{1}{2}$BC=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=$\frac{1}{2}$a(cm);
(3)MN=$\frac{1}{2}$b(cm),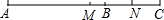
如图所示:
根据题意得:AB=b,
∴AC-BC=b,AM=MC=$\frac{1}{2}$AC,CN=BN=$\frac{1}{2}$CB,
∴NM=BM+BN=(MC-BC)+$\frac{1}{2}$BC
=($\frac{1}{2}$AC-BC)+$\frac{1}{2}$BC
=$\frac{1}{2}$AC+(-BC+$\frac{1}{2}$BC)
=$\frac{1}{2}$AC-$\frac{1}{2}$BC
=$\frac{1}{2}$(AC-BC)
=$\frac{1}{2}$b(cm).
点评 此题主要考查了线段的中点,关键是准确把握线段之间的倍数关系,理清线段之间的和差关系,进行等量代换即可.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:解答题
 如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
如图,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 分 组(m) | 频数(名) | 频率 |
| 1.565~1.595 | 2 | 0.04 |
| 1.595~1.625 | 4 | 0.08 |
| 1.6254~1.655 | 6 | 0.12 |
| 1.655~1.685 | 11 | 0.22 |
| 1.685~1.715 | 17 | 0.34 |
| 1.715~1.745 | 6 | 0.12 |
| 1.745~1.775 | 4 | 0.08 |
| 合 计 | 50 | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
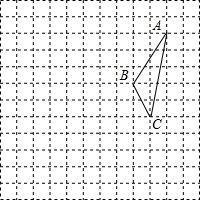 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC的顶点A、C的坐标分别是(4,7)、(3,2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
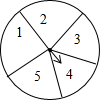 如图,有一个可以自由转动的转盘,被均匀分成5等份,分别标上1、2、3、4、5五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.
如图,有一个可以自由转动的转盘,被均匀分成5等份,分别标上1、2、3、4、5五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
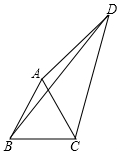 如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,
如图,四边形ABCD中,AC,BD是对角线,△ABC是等边三角形,∠ADC=30°,AD=3,BD=5,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com