
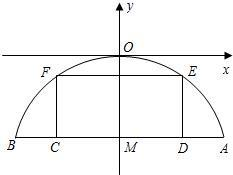
 有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为9米,货船在水面上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.分析 (1)根据题意设抛物线的解析式为y=ax2(a≠0).把已知坐标(9,-9)代入解析式求得a=-$\frac{1}{9}$,故抛物线的解析式为y=-$\frac{1}{9}$x2;
(2)已知CD=9,把已知坐标代入函数关系式可求解;
(3)设DM=a米,可得EF=CD=2DM=2a米、DE=FC=9-$\frac{1}{9}$a2,根据L=EF+DE+CF求得L的值最大时a的值,代入DE=9-$\frac{1}{9}$a2可得.
解答 解:(1)根据题意,设抛物线解析式为:y=ax2,
将点D(9,-9)代入,得:81a=-9,
解得:a=-$\frac{1}{9}$,
故抛物线解析式为:y=-$\frac{1}{9}$x2;
(2)当x=$\frac{9}{2}$时,y=-$\frac{1}{9}$×$\frac{81}{4}$=-$\frac{9}{4}$,
∵9-$\frac{9}{4}$=$\frac{27}{4}$,
∴矩形的高DE不能超过$\frac{27}{4}$米,才能使船通过拱桥;
(3)设DM=a米,则EF=CD=2DM=2a米,
当x=a时,y=-$\frac{1}{9}$a2,
∴DE=FC=9-$\frac{1}{9}$a2,
则L=2a+2(9-$\frac{1}{9}$a2)=-$\frac{2}{9}$a2+2a+18=-$\frac{2}{9}$(a-$\frac{9}{2}$)2+$\frac{45}{2}$,
∴当a=$\frac{9}{2}$时,L取得最大值,
当a=$\frac{9}{2}$时,矩形的高DE=FC=9-$\frac{1}{9}$a2=9-$\frac{1}{9}$×$\frac{81}{4}$=$\frac{27}{4}$(米).
点评 本题考查了运用待定系数法求二次函数的解析式及二次函数的应用,根据已知条件得出L的函数关系式及其最值情况是解决问题的关键.


科目:初中数学 来源: 题型:解答题
 解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.
解不等式组$\left\{\begin{array}{l}2x-1≤x+2,①\\ \frac{3x+1}{5}+2≥1.②\end{array}\right.$请结合题意填空,完成本题的解答.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
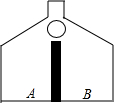 现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下.
现有一游戏装置如图所示,小球从最上方入口处投入,每次遇到黑色障碍物后,等可能地向左、右两边落下.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)
为纪念京汉铁路工人大罢工而修建的二七纪念塔于去年下半年重新整修,一装修工人站在塔的顶部处测得对面一栋AB=9米高的楼房的俯角为45°,测得楼房正前方18.2米处一站牌底部C点的俯角为60°,请你帮助装修工人计算塔的高度是多少?(已知装修工人身高为1.8米,眼部到头顶的距离和塔身的宽度都忽略不计,$\sqrt{3}$≈1.732,结果保留到1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
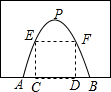 2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.
2015年以来.安徽省高速公路建设稳步推进,相继有十条高速公路建成通车.实现了所有的县在半小时内通达高速.全省高速公路通车里程突破4200公里.如图是某高速单向过山隧道截面设计图.隧道横截面呈抛物线形,设计AB=6米,最高点P点距地面8米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的角平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由.
如图,?ABCD中,O为BC边上一点,OD平分∠ADC,以O为圆心,OC为半径画圆,交OD于点E,若AB=6,?ABCD的面积是42$\sqrt{3}$,$\widehat{EC}$=π,请判断直线AB与⊙O的位置关系,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com