
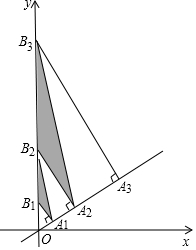
 如图,直线y=$\frac{{\sqrt{3}}}{3}$x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,分别过点A1,A2,A3,…An+1作直线y=$\frac{{\sqrt{3}}}{3}$x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为(22n-1-2n-1)$\sqrt{3}$.(用含正整数n的式子表示)
如图,直线y=$\frac{{\sqrt{3}}}{3}$x上有点A1,A2,A3,…An+1,且OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,分别过点A1,A2,A3,…An+1作直线y=$\frac{{\sqrt{3}}}{3}$x的垂线,交y轴于点B1,B2,B3,…Bn+1,依次连接A1B2,A2B3,A3B4,…AnBn+1,得到△A1B1B2,△A2B2B3,△A3B3B4,…,△AnBnBn+1,则△AnBnBn+1的面积为(22n-1-2n-1)$\sqrt{3}$.(用含正整数n的式子表示) 分析 由直线OAn的解析式可得出∠AnOBn=60°,结合AnAn+1=2n可求出AnBn的值,再根据三角形的面积公式即可求出△AnBnBn+1的面积.
解答 解:∵直线OAn的解析式y=$\frac{{\sqrt{3}}}{3}$x,
∴∠AnOBn=60°.
∵OA1=1,A1A2=2,A2A3=4,AnAn+1=2n,
∴A1B1=$\sqrt{3}$,A2B2=3$\sqrt{3}$,A3B3=7$\sqrt{3}$.
设S=1+2+4+…+2n-1,则2S=2+4+8+…+2n,
∴S=2S-S=(2+4+8+…+2n)-(1+2+4+…+2n-1)=2n-1,
∴AnBn=(2n-1)$\sqrt{3}$.
∴${S}_{△{A}_{n}{B}_{n}{B}_{n+1}}$=$\frac{1}{2}$AnBn•AnAn+1=$\frac{1}{2}$×(2n-1)$\sqrt{3}$×2n=(22n-1-2n-1)$\sqrt{3}$.
故答案为:(22n-1-2n-1)$\sqrt{3}$.
点评 本题考查了一次函数图象上点的坐标特征、三角形的面积、解直角三角形以及规律型中数的变化规律,根据边的变化找出变化规律“AnBn=(2n-1)$\sqrt{3}$”是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
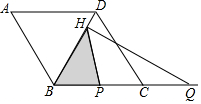 如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )
如图,菱形ABCD的边长为2,∠A=60°,点P和点Q分别从点B和点C出发,沿射线BC向右运动,且速度相同,过点Q作QH⊥BD,垂足为H,连接PH,设点P运动的距离为x(0<x≤2),△BPH的面积为S,则能反映S与x之间的函数关系的图象大致为 ( )| A. | 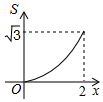 | B. | 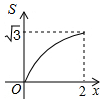 | C. | 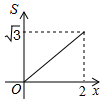 | D. | 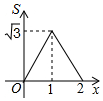 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
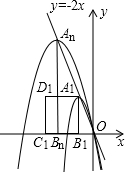 我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:
我们知道,经过原点的抛物线可以用y=ax2+bx(a≠0)表示,对于这样的抛物线:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
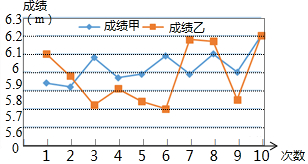 如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)
如图是甲、乙两名跳远运动员的10次测验成绩(单位:米)的折线统计图,观察图形,写出甲、乙这10次跳远成绩之间的大小关系:S甲2<S乙2(填“>“或“<”)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
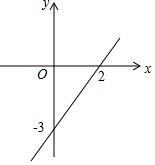 已知一次函数的图象如图所示.
已知一次函数的图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com