
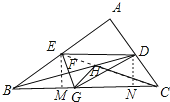
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2 ![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.
【答案】
(1)
解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
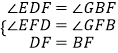 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形
(2)
解:作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,
在RT△EBM中,∵∠EMB=90°,∠EBM=30°,EB=ED=2 ![]() ,
,
∴EM= ![]() BE=
BE= ![]() ,
,
∵DE∥BC,EM⊥BC,DN⊥BC,
∴EM∥DN,EM=DN= ![]() ,MN=DE=2
,MN=DE=2 ![]() ,
,
在RT△DNC中,∵∠DNC=90°,∠DCN=45°,
∴∠NDC=∠NCD=45°,
∴DN=NC= ![]() ,
,
∴MC=3 ![]() ,
,
在RT△EMC中,∵∠EMC=90°,EM= ![]() .MC=3
.MC=3 ![]() ,
,
∴EC= ![]() =
= ![]() =10
=10 ![]() .
.
∵HG+HC=EH+HC=EC,
∴HG+HC的最小值为10 ![]()
【解析】(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.(2)作EM⊥BC于M,DN⊥BC于N,连接EC交BD于点H,此时HG+HC最小,在RT△EMC中,求出EM、MC即可解决问题.本题考查平行四边形的判定和性质、菱形的判定和性质、角平分线的性质、垂直平分线的性质、勾股定理等知识,解题的关键是利用对称找到点H的位置,属于中考常考题型.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法不正确的是( )
,下列说法不正确的是( )
A. 点(-2,-1)在它的图像上 B. 它的图像在第一、三象限
C. 当![]() 时,y随x的增大而增大 D. 当
时,y随x的增大而增大 D. 当![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】C
【解析】试题分析:反比例函数![]() 的性质:当
的性质:当![]() 时,图象在一、三象限,在每一象限,y随x的增大而减小;当
时,图象在一、三象限,在每一象限,y随x的增大而减小;当![]() 时,图象在二、四象限,在每一象限,y随x的增大而增大.
时,图象在二、四象限,在每一象限,y随x的增大而增大.
A.点![]() 在它的图象上,B.它的图象在第一、三象限,C.当
在它的图象上,B.它的图象在第一、三象限,C.当![]() 时,
时,![]() 随
随![]() 的增大而减小,均正确,不符合题意;
的增大而减小,均正确,不符合题意;
D.当![]() 时,
时,![]() 随
随![]() 的增大而减小,故错误,本选项符合题意.
的增大而减小,故错误,本选项符合题意.
考点:反比例函数的性质
点评:本题属于基础应用题,只需学生熟练掌握反比例函数的性质,即可完成.
【题型】单选题
【结束】
8
【题目】如图,双曲线![]() (x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )
(x<0)经过平行四边形ABCO的对角线交点D,已知边OC在y轴上,且AC⊥AB于点C,则平行四边形ABCO的面积是( )

A. ![]() B.
B. ![]() C. 3 D. 6
C. 3 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店为了迎接“读书节”制定了活动计划,陈经理查看计划书发现:A类图书的标价是B类图书标价的1.5倍,若顾客用1080元购买图书,能单独购买A类图书的数量恰好比单独购买B类图书的数量少20本.请求出A、B两类图书的标价.
【答案】A:27元、 B:18元
【解析】试题分析:设B类图书的标价是x元,则A类图书的标价是1.5x元,根据用1080元购买图书,单独购买A类图书的数量恰好比单独购买B类图书的数量少20本列出分式方程求解即可.
试题解析:
解:设B类图书的标价是x元,则A类图书的标价是1.5x元,
根据题意得: ![]() ,
,
去分母得:1620-1080=30x,
解得:x=18,
经检验x=18是原分式方程的解,
1.5x=27,
答:A、B两类图书的标价分别为27元、18元.
【题型】解答题
【结束】
25
【题目】如图,已知一次函数y1=kx+b的图象与反比例函数![]() 的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
的图象交于A、B两点, 且点A的坐标为(-2,3),点B的纵坐标是-2,求:
(1)一次函数与反比例函数的解析式;
(2)利用图像指出,当![]() 为何值时有
为何值时有![]() >
>![]() ;当
;当![]() 为何值时有
为何值时有![]() <
<![]()
(3)利用图像指出,当![]() >3时
>3时![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图□ABCD的对角线AC,BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=600,AB=![]() BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=
BC,连接OE .下列 结论:①∠CAD=300 ② S□ABCD=ABAC ③ OB=AB ④ OE=![]() BC 成立的个数有( )
BC 成立的个数有( )

A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用如图1的二维码可以进行身份识别.某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0.将第一行数字从左到右依次记为![]() ,
,![]() ,
,![]() ,
,![]() ,那么可以转换为该生所在班级序号,其序号为
,那么可以转换为该生所在班级序号,其序号为![]() .如图2第一行数字从左到右依次为0,1,0,1,序号为
.如图2第一行数字从左到右依次为0,1,0,1,序号为![]() ,表示该生为5班学生.表示6班学生的识别图案是( )
,表示该生为5班学生.表示6班学生的识别图案是( )


A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
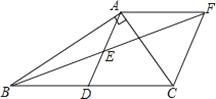
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=3,AB=4,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校一间阶梯教室中,第1排的座位数为a,从第2排开始,每一排都比前一排增加两个座位.
(1)请你在下表的空格里填写一个适当的式子:
第1排的 座位数 | 第2排的 座位数 | 第3排的 座位数 | 第4排的 座位数 | … |
a | a+2 | a+4 | … |
(2)写出第n排座位数的表达式;
(3)求当a=20时,第10排的座位数是多少?若这间阶梯教室共有15排,那么最多可容纳多少学员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,AD=3,M是边CD上一点,将△ADM沿直线AM对折,得到△ANM.
(1)当AN平分∠MAB时,求DM的长;
(2)连接BN,当DM=1时,求△ABN的面积;
(3)当射线BN交线段CD于点F时,求DF的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知代数式![]() ,当x=0时,该代数式的值为-1;
,当x=0时,该代数式的值为-1;
(1)求c的值;
(2)当x=1时,该代数式的值为-1,试求a+b+c的值;
(3)当x=3时,该代数式的值为9,试求当x=-3时该代数式的值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com