
【题目】已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.

(1)求证:FD是⊙O的切线;
(2)设OC与BE相交于点G,若OG=2,求⊙O半径的长;
(3)在(2)的条件下,当OE=3时,求图中阴影部分的面积.
【答案】(1)证明见解析(2)6;(3)![]()
【解析】
试题分析:(1)要证FD是⊙O的切线只要证明∠OCF=90°即可;
(2)根据已知证得△OEG∽△CBG根据相似比不难求得OC的长;
(3)根据S阴影=S△OCD﹣S扇形OBC从而求得阴影的面积.
证明:(1)连接OC(如图①),
∵OA=OC,
∴∠1=∠A.
∵OE⊥AC,
∴∠A+∠AOE=90°.
∴∠1+∠AOE=90°.
∵∠FCA=∠AOE,
∴∠1+∠FCA=90°.
即∠OCF=90°.
∴FD是⊙O的切线.
(2)连接BC,(如图②)
∵OE⊥AC,
∴AE=EC(垂径定理).
又∵AO=OB,
∴OE∥BC且![]() .
.
∴∠OEG=∠GBC(两直线平行,内错角相等),
∠EOG=∠GCB(两直线平行,内错角相等),
∴△OEG∽△CBG(AA).
∴![]() .
.
∵OG=2,
∴CG=4.
∴OC=OG+GC=2+4=6.
即⊙O半径是6.
(3)∵OE=3,由(2)知BC=2OE=6,
∵OB=OC=6,
∴△OBC是等边三角形.
∴∠COB=60°.
∵在Rt△OCD中,CD=OC×tan60°=6![]() ,
,
∴S阴影=S△OCD﹣S扇形OBC=![]() =
=![]() .
.




 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】(本题满分![]() 分)已知在平面直角坐标系
分)已知在平面直角坐标系![]() 中,点
中,点![]() 是抛物线
是抛物线![]() 上的一个动点,点
上的一个动点,点![]() 的坐标为
的坐标为![]() .
.
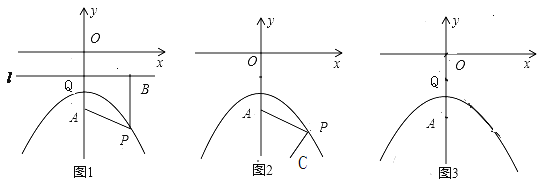
(1).如图1,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,过
轴,过![]() 点作
点作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,猜想
,猜想![]() 与
与![]() 的大小关系:
的大小关系: ![]() ______
______ ![]() (填写“>”“<”或“=” ),并证明你的猜想.
(填写“>”“<”或“=” ),并证明你的猜想.
(2).请利用(1)的结论解决下列问题:
①.如图2,设点![]() 的坐标为
的坐标为![]() , 连接
, 连接![]() ,问
,问![]() 是否存在最小值?如果存在,请说明理由,并求出点
是否存在最小值?如果存在,请说明理由,并求出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
②.若过动点![]() 和点
和点![]() 的直线交抛物线于另一点
的直线交抛物线于另一点![]() ,且
,且![]() ,求直线
,求直线![]() 的解析式(图3为备用图).
的解析式(图3为备用图).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.

(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂承接了一批纸箱加工任务,用如图1所示的长方形和正方形纸板(长方形的宽与正方形的边长相等)加工成如图所示的竖式与横式两种无盖的长方形纸箱.(加工时接缝材料不计)

若该厂购进正方形纸板1000张,长方形纸板2000张.问竖式纸盒,横式纸盒各加工多少个,恰好能将购进的纸板全部用完;
该工厂某一天使用的材料清单上显示,这天一共使用正方形纸板50张,长方形纸板a张,全部加工成上述两种纸盒,且120<a<136,试求在这一天加工两种纸盒时,a的所有可能值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com