
【题目】如图1所示,在正方形ABCD和正方形![]() 中,
中,![]() ,连结
,连结![]() .
.
(1)问题发现:![]() _________;
_________;
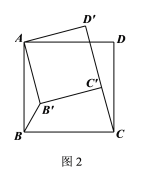
(2)拓展探究:将正方形![]() 绕点A逆时针旋转,记旋转角为
绕点A逆时针旋转,记旋转角为![]() ,连结
,连结![]() ,试判断:当
,试判断:当![]() ≤
≤![]()
![]() 时,
时,![]() 的值有无变化?请仅就图2中的情形给出你的证明;
的值有无变化?请仅就图2中的情形给出你的证明;
(3)问题解决:请直接写出在旋转过程中,当![]() 三点共线时
三点共线时![]() 的长.
的长.


【答案】(1)![]() ;(2)无变化,理由见解析;(3)
;(2)无变化,理由见解析;(3)![]() 的长为
的长为![]() 或
或![]()
【解析】
(1)延长![]() 交BC于点E,到等腰直角三角形,根据两直角边相等可得出结果
交BC于点E,到等腰直角三角形,根据两直角边相等可得出结果
(2) 先根据两个等腰直角三角形相似得出![]() ,根据这个条件可以得到△
,根据这个条件可以得到△![]() ∽△
∽△![]() ,就可以得出结论。
,就可以得出结论。
(3)![]() 共线分两种情况,根据旋转角度的不同进行分类讨论。
共线分两种情况,根据旋转角度的不同进行分类讨论。
(1)![]() ;
;
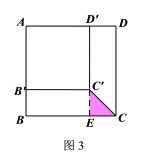
提示:延长![]() 交BC于点E,如图3所示.
交BC于点E,如图3所示.
则![]() ,△
,△![]() 为等腰直角三角形
为等腰直角三角形
∴![]()
∴![]() .
.
(2)无变化;
理由如下:连结AC、![]() ,如图4所示.
,如图4所示.
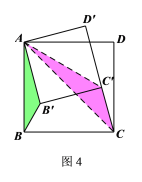
∵△ABC和△![]() 均为等腰直角三角形
均为等腰直角三角形
∴![]()
∵![]()
∴![]()
∴△![]() ∽△
∽△![]()
∴![]()
∴当![]() ≤
≤![]() <360°时,
<360°时,![]() 的值无变化;
的值无变化;
(3)![]() 的长为
的长为![]() 或
或![]() .
.
提示:分为两种情况:
①如图5所示,连结AC.
![]()
在Rt△![]() 中,由勾股定理得:
中,由勾股定理得:
![]()
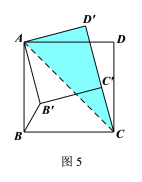
∴![]()
∵![]()
∴![]() ;
;
②如图6所示,
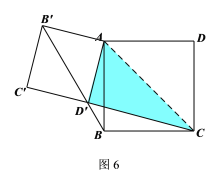
此时![]()
∵![]()
∴![]() .
.
综上所述,![]() 的长为
的长为![]() 或
或![]() .
.


 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() 且开口向下,则下列结论:①抛物线经过点
且开口向下,则下列结论:①抛物线经过点![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④对于任意实数
有两个不相等的实数根;④对于任意实数![]() ,
,![]() 总成立。其中结论正确的个数为( )
总成立。其中结论正确的个数为( )
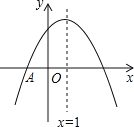
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠ABC=90°.
(1)尺规作图:按下列要求完成作图(保留作图痕迹,请标明字母)
①作线段AC的垂直平分线l,交AC于点O;
②连接BO并延长,在BO的延长线上截取OD,使得OD=OB;
③连接DA、DC.
(2)判断四边形ABCD的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
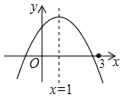
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
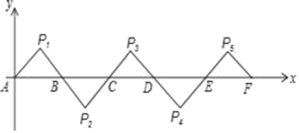
【题目】如图所示,在平面直角坐标系中,A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C,把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,得到的等腰直角三角形的直角顶点P2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有两枚质地均匀的正方体骰子,每枚骰子的六个面上都分别标有数字1、2、3、4、5、6.同时投掷这两枚骰子,以朝上一面所标的数字为掷得的结果,那么所得结果之和为9的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,点
,点![]() 是点
是点![]() 以
以![]() 为对称中心的对称点,点
为对称中心的对称点,点![]() 运动的同时,点
运动的同时,点![]() 从
从![]() 出发沿
出发沿![]() 向
向![]() 运动,速度为每秒
运动,速度为每秒![]() ,当点
,当点![]() 到达顶点
到达顶点![]() 时,
时,![]() 同时停止运动,设
同时停止运动,设![]() 两点运动时间为
两点运动时间为![]() 秒.
秒.
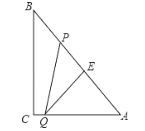
(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)四边形![]() 面积能否是
面积能否是![]() 面积的
面积的![]() ?若能,求出此时
?若能,求出此时![]() 的值;若不能,请说明理由;
的值;若不能,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() 为等腰三角形?(直接写出结果)
为等腰三角形?(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,斜边
,斜边![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() ,连接
,连接![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速行动,速度为
方向匀速行动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停让运动.连接
;当一个点停止运动,另一个点也停让运动.连接![]() ,
,![]() ,
,![]() 交
交![]() 于点
于点![]() .设运动时间为
.设运动时间为![]() ,解答下列问题:
,解答下列问题:
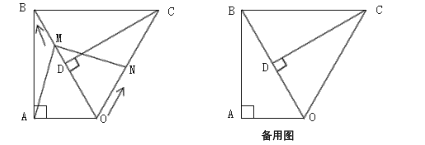
(1)当![]() 为何值时,
为何值时,![]() 平分
平分![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函教关系式;
的函教关系式;
(3)在运动过程中,当![]() 时,求四边形
时,求四边形![]() 的面积;
的面积;
(4)在运动过程中,是否存在某一时刻![]() ,使点
,使点![]() 为线段
为线段![]() 的中点?若存在,求出
的中点?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com