
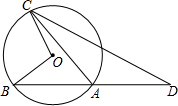
 如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.
如图,点O为$\widehat{BC}$所在圆的圆心,∠BOC=112°,点D在BA的延长线上,AD=AC,则∠D=28°.  备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
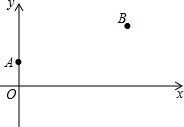 如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.
如图所示,A,B两村在某条河的同侧,以河岸为x轴,建立直角坐标系,A,B两村相对应的坐标为(0,1),(4,2)(长度单位为km).现在要在河岸的P点处直接向A,B两村送水,则点P选在何处才能使所用的水管最短?试写出点P的坐标及所需水管的长度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com