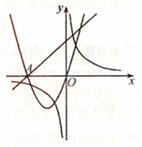
一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=k/x在同一直角坐标系中的图像如图所示，A点的坐标为（－2，0），则下列结论中，正确的是 （ ）
A．b=2a+k B．a=b+k C．a>b>0 D．a>k>0
科目：初中数学 来源： 题型：
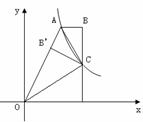
如图，双曲线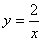
（x＞0）经过四边形OABC的顶点A、C，∠ABC＝90°，OC平分OA与
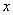轴正半轴的夹角，AB∥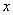轴，将△ABC沿AC翻折后得到△AB＇C，B＇点落在OA上，则四边形OABC的面积是（ ）．
A．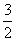
B．
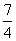C．2 D．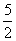
| |
查看答案和解析>>
科目：初中数学 来源： 题型：
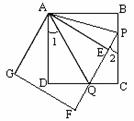
如图，正方形ABCD的边长为3，将正方形ABCD绕点A顺时针旋转角度α（0°＜α＜90°），得到正方形AEFG，FE交线段DC于点Q，FE的延长线交线段BC于点P，连结AP、AQ．
（1）求证：△ADQ≌△AEQ；
（2）求证：PQ＝DQ＋PB；
（3）当∠1=∠2时，求PQ的长．（杭十五中模拟）
查看答案和解析>>
科目：初中数学 来源： 题型：
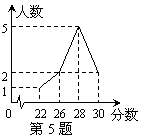
在“体育中考”的某次模拟测试中，某校某班10名学生测试成绩统计如图所示．对于这10名学生的参赛成绩，下列说法中错误的是 （ ）
A．众数是90 B．中位数是28 C．平均数是27.5 D．极差是8
查看答案和解析>>
科目：初中数学 来源： 题型：
在平面直角坐标系中，有反比例函数y =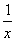 
与y = 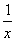－ 的图象和正方形ABCD，原点O 与对角线AC、BD的交点重叠，且如图所示的阴影部分面积为8，则AB= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
如图,已知在等腰△ABC中,∠A=∠B=30°,过点C作CD⊥AC交AB于点D.
(1)尺规作图：过A，D，C三点作⊙O（只要求作出图形，保留痕迹，不要求写作法）；
(2)求证：BC是过A，D，C三点的圆的切线；
(3)若过A，D，C三点的圆的半径为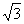
,则线段BC上是否存在一点P，使得以P，D，B为顶点的三角形与△BCO相似.若存在，求出DP的长；若不存在，请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
以下哪些选项可判断二次函数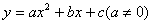
与x轴有两个交点：__________（只需填上正确的序号）
①a+b+c=0；②b＞a+c；③b= 2a+3c；④ac＜0
查看答案和解析>>
科目：初中数学 来源： 题型：
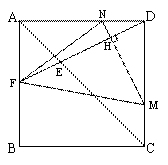
如图，正方形ABCD中，AB=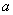
（单位：cm），点E、M分别是线段AC，CD上的动点，连结DE并延长交正方形的边于点F，过点M作MN⊥DF于H，交AD于N。点M从点C出发，以1cm/s的速度沿CD向点D运动，点E从点A出发，以
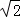cm/s速度沿AC向点C运动，运动时间为
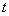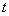（＞0）；下列判断正确的是：（ ）
①当M不动，E运动时，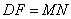
；
②当M,E同时出发时，且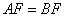
时，点M是边CD的三等分点；
③当M,E同时出发时，且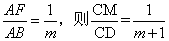
④当M,E同时出发后，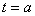
或
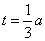时，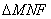
为等腰三角形；
A.①②④ B.①③ C.①②③ D①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
B．
D．