
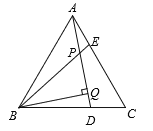
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
【答案】(1)见解析;(2)PE=1.
【解析】
(1)根据等边三角形的性质得到AB=AC,∠BAE=∠C=60°,证明△ABE≌△CAD
(2)根据直角三角形的性质得到BP=2PQ,再根据题意BP=2PQ =4,则PE =1.
(1)∵△ABC是等边三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中, ,
,
∴△ABE≌△CAD(SAS),
(2) ∵△ABE≌△CAD,
∴∠ABE=∠CAQ,
∴∠BPQ=∠BAP+∠ABE=∠BAP+∠CAD=∠BAC=60°,∵BQ⊥AD,
∴∠PBQ=90°∠BPQ=90°60°=30°,
∴BP=2PQ.
∵PQ=2,BE=5,
则BP=2PQ =4,PE = BE- PB=5-4=1.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】3 月初某商品价格上涨,每件价格上涨 20%.用 3000 元买到的该商品 件数比涨价前少 20 件.3 月下旬该商品开始降价,经过两次降价后,该商品价格为每 件 19.2 元.
(1)求 3 月初该商品上涨后的价格;
(2)若该商品两次降价率相同,求该商品价格的平均降价率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC底边BC上的高为16 cm,当BC的长x(cm)从小到大变化时,△ABC的面积y(cm2)也随之发生变化.
(1)在这个变化过程中,常量是________,自变量是________,因变量是_________;
(2)写出y与x之间的关系式为_______________;
(3)当x=5 cm时,y=________cm2;当x=15 cm时,y=________cm2;y随x的增大而__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小淇在说明 “直角三角形斜边上的中线等于斜边的一半”是真命题,部分思路如下:如图,在∠ACB内做∠BCD=∠B,CD与AB相交于点D,…….请根据以上思路,完成证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
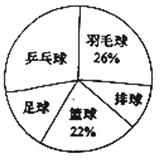
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
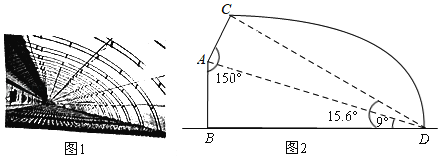
【题目】随着我市农产品整体品牌形象“聊胜一筹!”的推出,现代农业得到了更快发展.某农场为扩大生产建设了一批新型钢管装配式大棚,如图1.线段AB,BD分别表示大棚的墙高和跨度,AC表示保温板的长.已知墙高AB为2米,墙面与保温板所成的角∠BAC=150°,在点D处测得A点、C点的仰角分别为9°,15.6°,如图2.求保温板AC的长是多少米?(精确到0.1米)
(参考数据:![]() ≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
≈0.86,sin9°≈0.16,cos9°≈0.99,tan9°≈0.16,sin15.6°≈0.27,cos15.6°≈0.96,tan15.6°≈0.28)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com