
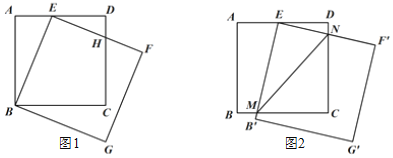
【题目】如图1,在正方形ABCD中,AB=3,E是AD边上的一点(E与A、D不重合),以BE为边画正方形BEFG,边EF与边CD交于点H.
(1)当E为边AD的中点时,求DH的长;
(2)设DE=x,CH=y,求y与x之间的函数关系式,并求出y的最小值;
(3)若DE=![]() ,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
,将正方形BEFG绕点E逆时针旋转适当角度后得到正方形B'EF'G',如图2,边EF'与CD交于点N、EB'与BC交于点M,连结MN,求∠ENM的度数.
【答案】(1)DH=![]() ; (2)
; (2) ![]() ,y的最小值为
,y的最小值为![]() ;(3)∠ENM=60°.
;(3)∠ENM=60°.
【解析】
(1)根据正方形的性质得到∠D=∠A=∠BEF=90°,根据余角的性质得到∠AEB=∠DHE,根据相似三角形的想知道的![]() ,代入数据即可得到结论;
,代入数据即可得到结论;
(2) 由第一题的比值代入得![]() ,化简整理成二次函数即可,再求出函数的极值;
,化简整理成二次函数即可,再求出函数的极值;
(3)通过作辅助线,可证△PMC∽△PDE, △PCE∽△PMN,得到∠EMN=∠ECN,从而可在△CED中,求得tan∠ECD值,从而求得∠ECD 角度,∠EMN=∠ECD=30°,所以在Rt△EMN中,利用互余求∠ENM=90°-30°=60°.
∵四边形ABCD和四边形BGFE是正方形,
∴∠D=∠A=∠BEF=90°,
∴∠AEB+∠DEH=∠DEH+∠DHE=90°,
∴∠AEB=∠DHE,
∴△EDH∽△BAE,
∴![]() ,
,
∵E为边AD的中点,
∴DE=AE=1.5,
∴![]() ,
,
∴DH=![]() .
.
由上得,![]() ,
,
∴![]() ,
,
∴![]() (2分)=
(2分)=![]() .
.
∵![]() >0,
>0,
∴y的最小值为![]() .
.
(3)
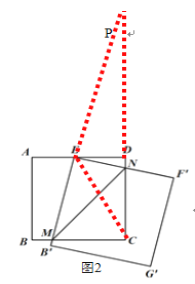
连结CE,延长ME、CD,两线交于点P,
∵在正方形ABCD中,AD∥BC
∴△PMC∽△PED,
∴![]()
变换得:![]()
又∵在Rt△PEN中,![]()
∴![]()
又∵∠P=∠P公共角
∴△PCE∽△PMN,
∴∠EMN=∠ECN
又∵在Rt△CED中,求得tan∠ECD=![]() =
=![]() ,
,
∴∠ECD=30°
∴∠EMN=∠ECD=30°,
∴在Rt△EMN中,∠ENM=90-30°=60°.


科目:初中数学 来源: 题型:
【题目】某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单价70元/个.
(1)原计划募捐3400元,购买两种款式的书包共60个,那么这两种款式的书包各买多少个?
(2)在捐款活动中,由于学生捐款的积极性高涨,实际共捐款4800元,如果至少购买两种款式的书包共80个,那么女款书包最多能买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次安全知识测验中,学生得分均为整数,满分10分,成绩达到9分为优秀,这次测验中甲、乙两组学生人数相同,成绩如下两个统计图:
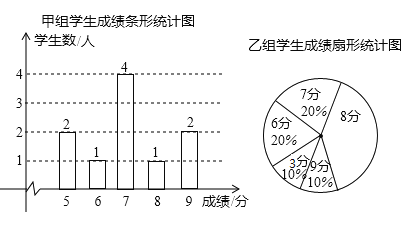
(1)在乙组学生成绩统计图中,8分所在的扇形的圆心角为 度;
(2)请补充完整下面的成绩统计分析表:
平均分 | 方差 | 众数 | 中位数 | 优秀率 | |
甲组 | 7 | 1.8 | 7 | 7 | 20% |
乙组 | 10% |
(3)甲组学生说他们的优秀率高于乙组,所以他们的成绩好于乙组,但乙组学生不同意甲组学生的说法,认为他们组的成绩要好于甲组,请你给出两条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区为了解全区2800名九年级学生英语口语考试成绩的情况,从中随机抽取了部分学生的成绩(满分24分,得分均为整数),制成下表:
分数段(x分) | x≤16 | 17≤x≤18 | 19≤x≤20 | 21≤x≤22 | 23≤x≤24 |
人 数 | 10 | 15 | 35 | 112 | 128 |
(1)填空:
①本次抽样调查共抽取了 名学生;
②学生成绩的中位数落在 分数段;
③若用扇形统计图表示统计结果,则分数段为x≤16的人数所对应扇形的圆心角为 °;
(2)如果将21分以上(含21分)定为优秀,请估计该区九年级考生成绩为优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
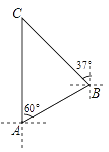
【题目】知识改变世界,科技改变生活.导航装备的不断更新极大方便了人们的出行.如图,某校组织学生乘车到黑龙滩(用C表示)开展社会实践活动,车到达A地后,发现C地恰好在A地的正北方向,且距离A地13千米,导航显示车辆应沿北偏东60°方向行驶至B地,再沿北偏西37°方向行驶一段距离才能到达C地,求B、C两地的距离.(参考数据:sin53°≈![]() ,cos53°≈
,cos53°≈![]() ,tan53°≈
,tan53°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“三等分任意角”是数学史上一个著名问题,经过无数人探索,现在已经确信,仅用圆规直尺是不可能做出的.在探索过程中,我们发现,可以利用一些特殊的图形,把一个任意角三等分.如图:在∠MAN的边上任取一点B,过点B作BC⊥AN于点C,并作BC的垂线BF,连接AF,E是AF上一点,当AB=BE=EF时,有∠FAN=![]() ∠MAN,请你证明.
∠MAN,请你证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年6月,某市全面推进生活垃圾分类工作.如图是某小区放置的垃圾桶,从左到右依次是红色:有害垃圾;蓝色:可回收垃圾;绿色:厨余垃圾;黑色:其他垃圾.

(1)居民A将一袋厨余垃圾随手放入一个垃圾桶,问他能正确投放垃圾的概率是 .
(2)居民B手拎两袋垃圾,一袋是可回收垃圾,另一袋是有害垃圾。她先将可回收垃圾随手放入一个垃圾桶,然后把另一袋垃圾又随手放入其他垃圾桶。问:两袋垃圾都投放错误的概率?请画出树状图或列表说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个大小,质地都相同的乒乓球,球面上分别标有数字1,-2,3,-4,小明先从布袋中随机摸出一个球(不放回去),再从剩下的3个球中随机摸出第二个乒乓球.
(1)共有 种可能的结果.
(2)请用画树状图或列表的方法求两次摸出的乒乓球的数字之积为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com