
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
【答案】解:(1)证明:∵四边形ABCD是矩形,∴DC∥AB。
∴∠OAE=∠OCF,∠OEA=∠OFC。
又∵AE=CF,∴△OEA≌△OFC(ASA)。
∴OE=OF。
(2)如图,连接OB,

∵BE=BF,OE=OF,∴BO⊥EF,∠ABO=∠OBF。
∵∠BEF=2∠BAC,∴∠OBE=∠BAC。
又∵矩形ABCD中,∠ABC=900,∴∠BOE=∠ABC=900。
∴△OBE∽△BAC。∴![]() 。
。
∵∠BEF=2∠BAC,∴∠OAE=∠AOE。∴AE=OE。
设AB=x,AE=OE=y,则![]() 。
。
∵BC=![]() ,∴
,∴![]() 。
。
由(1)△OEA≌△OFC,得AO=CO,∴![]() 。
。
∴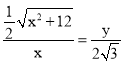 。∴
。∴![]() ①。
①。
又∵![]() ,即
,即![]() ,
,
化简,得![]() ②。
②。
由①②得![]() ,两边平方并化简,得
,两边平方并化简,得![]() ,
,
∴![]() ,∴根据x的实际意义,得x=6。
,∴根据x的实际意义,得x=6。
∴若BC=![]() , AB的长为6。
, AB的长为6。
【解析】试题分析:(1)根据△AEO和△CFO全等来进行说明;(2)连接OB,得出△BOF和△BOE全等,然后求出∠BAC的度数,根据∠BAC的正切值求出AB的长度.
试题解析:(1)∵四边形ABCD是矩形,∴AB∥CD ∴∠OAE=∠OCF ∠OEA=∠OFC ∵AE=CF
∴△AEO≌△CFO ∴OE=OF
(2)连接BO ∵OE=OF BE=BF
∴BO⊥EF 且∠EBO=∠FBO ∴∠BOF=90°
∵四边形ABCD是矩形
∴∠BCF=90°
∵∠BEF=2∠BAC ∠BEF=∠BAC+∠EOA
∴∠BAC=∠EOA AE=OE
∵AE=CF OE=OF
∴OF=CF 又∵BF=BF
∴Rt△BOF≌Rt△BCF
∴∠OBF=∠CBF
∴∠CBF=∠FBO=∠OBE
∵∠ABC=90° ∠OBE=30°
∴∠BEO=60° ∠BAC=30°
∵tan∠BAC=![]()
∴tan30°=![]() 即
即![]() ∴AB=6.
∴AB=6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠3=∠B,∠4=65°,求证∠ACB=∠4.请填空完
成证明过程:

∵∠1+∠2=180°( )∠1+∠______=180°
∴∠2=∠DFE( )
∴AB∥EF( )
∴∠3=∠ADE( )
又∵∠3=∠B
∴∠ADE=∠_______
∴DE∥BC( )
∴∠ACB=∠4( )
∴∠ACB=65°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AC,BD相交于点O,O是AC的中点,AD//BC,AC=8,BD=6.
(1)求证:四边形ABCD是平行四边形;
(2)若AC⊥BD,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好宣传“开车不喝酒,喝酒不开车”的驾车理念,某市一家报社设计了如图1的调查问卷(单选),在随机调查了本市10000名司机中的部分司机后,统计整理并制作了如图2所示的统计图: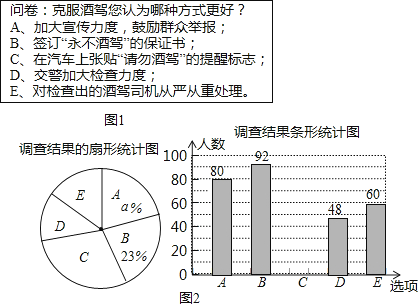
根据以上的信息解答下列问题:
(1)补全条形统计图,并计算扇形统计图中a= .
(2)该市支持选项C的司机大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,根据2013﹣2017年某市财政总收入(单位:亿元)统计图所提供的信息,下列判断正确的是( )
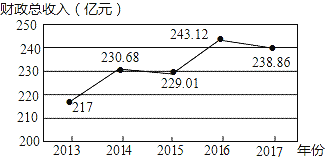
A. 2013~2017年财政总收入呈逐年增长
B. 预计2018年的财政总收入约为253.43亿元
C. 2014~2015年与2016~2017年的财政总收入下降率相同
D. 2013~2014年的财政总收入增长率约为6.3%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与点A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能请直接写出点P坐标,若不能请说明理由;
(4)在抛物线对称轴上是否存在点M使|MA﹣MC|最大?若存在请求出点M的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形A1B1B2C1 , A2B2B3C2 , A3B3B4C3 , …,AnBnBn+1Cn , 按如图所示放置,使点A1、A2、A3、A4、…、An在射线OA上,点B1、B2、B3、B4、…、Bn在射线OB上.若∠AOB=45°,OB1=1,图中阴影部分三角形的面积由小到大依次记作S1 , S2 , S3 , …,Sn , 则Sn= . 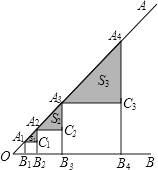
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com