
分析 (1)去括号,移项,合并同类项,系数化成1即可;
(2)去分母,去括号,移项,合并同类项,系数化成1即可;
(3)去分母,去括号,移项,合并同类项,系数化成1即可;
(4)去分母,去括号,移项,合并同类项,系数化成1即可.
解答 解:(1)12-3(9-x)=5(x-4)-7(7-x),
12-27+3x=5x-20-49+7x,
3x-5x-7x=-20-49-12+27,
-9x=-54,
x=6;
(2)$\frac{3x+2}{3}$-1=$\frac{7x-3}{5}$+$\frac{2(x-2)}{15}$,
5(3x+2)-15=3(7x-3)+2(x-2),
15x+10-15=21x-9+2x-4,
15x-21x-2x=-9-4-10+15,
-8x=-8,
x=1;
(3)$\frac{x+0.4}{0.2}$-$\frac{x-3}{0.5}$=2,
5x+2-(2x-6)=2,
5x+2-2x+6=2,
3x=-6,
x=-2;
(4)$\frac{2x-1}{4}$=$\frac{2}{3}$x-2,
3(2x-1)=8x-24,
6x-3=8x-24,
6x-8x=-24+3,
-2x=-21,
x=$\frac{21}{2}$.
点评 本题考查了解一元一次方程的应用,能正确根据等式的性质进行变形是解此题的关键.


科目:初中数学 来源: 题型:解答题
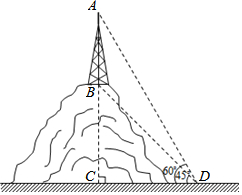 如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).
如图,某山顶上建有手机信号中转塔AB,在地面D处测得塔尖的仰角∠ADC=60°,塔底的仰角∠BDC=45°,点D距离塔AB所在直线的距离DC为100米,求手机信号中转塔AB的高度(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
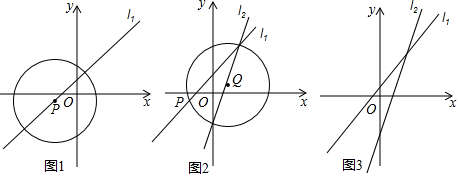
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为-1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
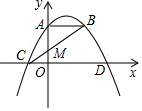 如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D.
如图,点A是y轴上的点,线段AB∥x轴,M是OA的中点,连接BM并延长交x轴与点C,二次函数y=ax2-2ax+4的图象经过A,B,C的三点,与x轴的另一交点为D.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200-2x | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.
如图,在△ABC中,DE∥BC,AD=4,DE=3,DB=8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com