练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．按要求做题
    （1）解不等式：5（x-2）＞8x-4
    （2）分解因式：am2-2am+a．

    分析 （1）根据解一元一次不等式的方法步骤，去括号，移项，合并同类项，系数化为1，即可得出结果；
    （2）首先用提取公因式法分解因式，再运用完全平方公式分解因式即可．

    解答 解：（1）5（x-2）＞8x-4
    去括号得：5x-10＞8x-4，
    移项得：5x-8x＞-4+10
    合并同类项得：-3x＞6
    系数化为1得：x＜-2；
    （2）am2-2am+a
    =a（m2-2m+1）
    =a（m-1）2．

    点评 本题考查了一元一次不等式的解法、因式分解的方法；熟练掌握一元一次不等式的解法和因式分解的方法是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

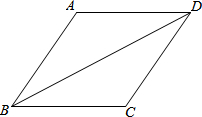    9．如图，在四边形ABCD中，∠BCD是钝角，AB=AD，BD平分∠ABC，若CD=3，BD=$2\sqrt{6}$，sin∠DBC=$\frac{{\sqrt{3}}}{3}$，求对角线AC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．下列说法正确的是（　　）
    A．单项式乘以多项式的积可能是一个多项式，也可能是单项式
    B．单项式乘以多项式的积仍是一个单项式
    C．单项式乘以多项式的结果的项数与原多项式的项数相同
    D．单项式乘以多项式的结果的项数与原多项式的项数不同

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．解下列不等式（组），并用数轴表示解集
    （1）$\frac{1}{2}$（3y-1）-$\frac{1}{5}y$＜y+1
    （2）$\left\{\begin{array}{l}{-2x+1＞-11}\\{\frac{3x+1}{2}-1≥x}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．甲乙两工程队同时修路，两队所修路的长度相等，甲队施工速度一直没变，乙队在修了3小时后加快了修路速度，在修了5小时后，乙又因故施工速度减少到每小时5米，如图所示是两队所修公路长度y（米）与所修时间x（小时）的图象，请回答下列问题．
    （1）直接写出甲队在0≤x≤5时间段内，y与x的函数关系式为y=14x；直接写出乙队在3≤x≤5时间段内，y与x的函数关系式为y=35x-85；
    （2）求开修多长时间后，乙队修的长度超过甲队10米；
    （3）如最后两队同时完成任务，求乙队从开修到完工所修长度为多少米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．某校运动会需购买A、B两种奖品共100件．若A种奖品每件10元，B种奖品每件15元，设购买A、B两种奖品的总费用为W元，购买A种奖品m件．
    （1）求出W（元）与m（件）之间的函数关系式；
    （2）若总费用不超过1150元，且A种奖品的数量不大于B种奖品数量的3倍，试求出最少费用W的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．若2xa+b-3y3a+2b-4=8是关于x，y的二元一次方程，则a=3，b=-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．已知二次一次方程组$\left\{\begin{array}{l}{m-2n=4}\\{2m-n=3}\end{array}\right.$，则m+n的值是（　　）
    A．-1B．0C．1D．-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．请阅读下列材料：
    问题：已知方程x2+x-1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
    解：设所求方程的根为y，则y=2x，所以x=$\frac{y}{2}$．
    把x=$\frac{y}{2}$代入已知方程，得（$\frac{y}{2}$）2+$\frac{y}{2}$-1=0．
    化简，得y2+2y-4=0
    故所求方程为y2+2y-4=0．
    这种利用方程的代换求新方程的方法，我们称为“换根法”．
    请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）．
    （1）已知方程x2+x-2=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为：y2-y-2=0．
    （2）已知方程2x2-7x+3=0，求一个一元二次方程，使它的根分别是已知方程根的倒数．
    （3）已知关于x的一元二次方程ax2+bx+c=0（a≠0）的两个实数根分别为3，-2，求一元二次方程cx2+bx+a=0的两根．（直接写出结果）

    查看答案和解析>>

    同步练习册答案