
已知:抛物线y1=x2以点C为顶点且过点B,抛物线y2=a2x2+b2x+c2以点B为顶点且过点C,分别过点B、C作x轴的平行线,交抛物线y1=x2、y2=a2x2+b2x+c2于点D,且AB=AC.
(1)如图,①求证△ABC为正三角形;②求点A的坐标;
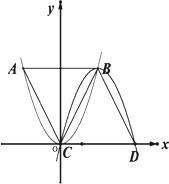
(2)①如图,若将抛物线“y1=x2”改为“y1=x2+1”,其他条件不变,求CD的长;

②如图,若将抛物线“y1=x2”改为“y1=3x2+b1x+c1”,其他条件不变,求a2的值;
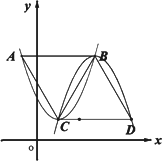
(3)若将抛物线“y1=x2”改为抛物线“y1=a1x2+b1x+c1”,其他条件不变,直接写出b1关于b2的关系式.
 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源:2012届河南信阳市二中中考模拟考试数学试卷(带解析) 题型:解答题
已知:抛物线 (a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,
(a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0, ),与x轴交于A、B两点(A在B的左边).
),与x轴交于A、B两点(A在B的左边).
(1)求此抛物线的表达式;
(2)点P是线段OB上一动点(不与点B重合),点Q在线段BM上移动且∠MPQ=45°,设线段OP=x,MQ= 1,求y1与x的函数关系式,并写出自变量x的取值范围;
1,求y1与x的函数关系式,并写出自变量x的取值范围;
(3)①在(2)的条件下是否存在点P,使△PQB是PB为底的等腰三角形,若存在试求点Q的坐标,若不存在说明理由;
②在(1)中抛物线的对称轴上是否存在点F,使△BMF是等腰三角形,若存在直接写出所有满足条件的点F的坐标.
查看答案和解析>>
科目:初中数学 来源:2013届江苏省无锡市育才中学九年级上学期期末考试数学试卷(带解析) 题型:解答题
已知:抛物线y1=-2x2+2与直线y2=2x+2相交
点A和点B, 
(1)求出点A和点B的坐标。
(2)观察图象,请直接写出y1>y2的自变量x的取值范围。
(3)当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,
取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.(例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.) 求:使得M=1的x值。=】
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省无锡市九年级上学期期末考试数学试卷(解析版) 题型:解答题
已知:抛物线y1=-2x2+2与直线y2=2x+2相交
点A和点B,
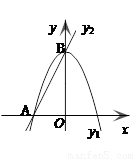
(1)求出点A和点B的坐标。
(2)观察图象,请直接写出y1>y2的自变量x的取值范围。
(3)当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,
取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.(例如:当x=1时,y1=0,y2=4,y1<y2,此时M=0.) 求:使得M=1的x值。=】
查看答案和解析>>
科目:初中数学 来源:2011-2012学年河南信阳市二中中考模拟考试数学试卷(解析版) 题型:解答题
已知:抛物线 (a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0,
(a≠0)的顶点M的坐标为(1,-2)与y轴交于点C(0, ),与x轴交于A、B两点(A在B的左边).
),与x轴交于A、B两点(A在B的左边).

(1)求此抛物线的表达式;
(2)点P是线段OB上一动点(不与点B重合),点Q在线段BM上移动且∠MPQ=45°,设线段OP=x,MQ= 1,求y1与x的函数关系式,并写出自变量x的取值范围;
1,求y1与x的函数关系式,并写出自变量x的取值范围;
(3)①在(2)的条件下是否存在点P,使△PQB是PB为底的等腰三角形,若存在试求点Q的坐标,若不存在说明理由;
②在(1)中抛物线的对称轴上是否存在点F,使△BMF是等腰三角形,若存在直接写出所有满足条件的点F的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com