
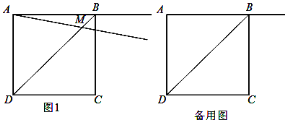
【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
【答案】(1)①补图见解析,证明见解析;②![]() ;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,
;(2)①当0°<α<45°时,∠NCE=2∠BAM;②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
【解析】(1)①补全的图形即可.先证明△ABM≌△CBM得AM=MC,再根据点N与点M关于直线CE对称得CM=CN,即可得到结论;
②由平行线的性质得到∠AMD=∠ANC,又由等腰三角形的性质得到∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,从而∠AMD=∠CMD,进一步得到∠CMN=∠AMD=∠CMD=60°,∠ADB=45°,过点A作AG⊥BD,根据边长为2,可以求出DM的长.
(2)分两种情况讨论:①当0°<α<45°时,∠NCE=2∠BAM.作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.由△ABM≌△CBM,可得∠BAM=∠BCM,由∠ABC=∠CEA=90°,BC,AE交于一点,可得∠BAM=∠BCE,即可得到∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,即可得到∠NCE=∠MCE,进而得出∠NCE=2∠BAM.
②当45°<α<90°时,![]() .连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即
.连接CM,判定△ADM≌△CDM,即可得到∠DAM=∠DCM,再根据∠DAQ=∠ECQ,即可得到∠NCE=∠MCE=2∠DAQ,即![]() ,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到
,再根据∠BAM=∠BCM,∠BCM+∠DCM=90°,即可得到![]() .
.
(1)①补全的图形如图所示.
∵ABCD是正方形,∴AB=BC,∠ABM=∠CBM,BM=BM,∴△ABM≌△CBM,∴AM=MC.
∵点N与点M关于直线CE对称,∴CM=CN,∴AM=CN;
②∵BD∥CN,∴∠AMD=∠ANC.
又∵CM=CN,∴∠CMN=∠CNM,由①中△ABM≌△CBM得∠AMB=∠CMB,∴∠AMD=∠CMD,∴∠CMN=∠AMD=∠CMD=60°,∠ADB=45°.
过点A作AG⊥BD.
∵AD=2,∠ADG=45°,∴AG=DG=![]() .
.
∵∠AMD=60°,∴∠MAG=30°,∴MG=![]() ,∴DM=
,∴DM=![]() .
.
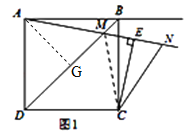
(2)①当0°<α<45°时,NCE=2∠BAM.
如图1,连接MC,∵△ABM≌△CBM,∴∠BAM=∠BCM,∵∠ABC=∠CEA=90°,BC,AE交于一点,∴∠BAM=∠BCE,∴∠MCE=2∠BAM,由点N与点M关于直线CE对称,可得CN=CM,∴∠NCE=∠MCE,∴∠NCE=2∠BAM.
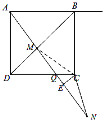
②当45°<α<90°时,![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.
如图,连接CM,∵AD=CD,∠ADM=∠CDM,DM=DM,∴△ADM≌△CDM,∴∠DAM=∠DCM.
∵∠ADQ=∠CEQ=90°,∠AQD=∠CQE,∴∠DAQ=∠ECQ,∴∠NCE=∠MCE=2∠DAQ,∴∠DCM=![]() ∠NCE.
∠NCE.
∵∠BAM=∠BCM,∠BCM+∠DCM=90°,∴![]() ∠NCE+∠BAM=90°.
∠NCE+∠BAM=90°.


科目:初中数学 来源: 题型:
【题目】水果批发市场有一种高档水果,如果每千克盈利(毛利润)10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销量将减少20千克.
(1)若以每千克能盈利18元的单价出售,问每天的总毛利润为多少元?
(2)现市场要保证每天总毛利润6000元,同时又要使顾客得到实惠,则每千克应涨价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=kx+b与双曲线y2= ![]() 交于A、B两点,它们的横坐标分别为1和5.
交于A、B两点,它们的横坐标分别为1和5. 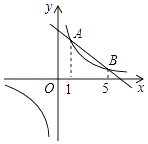
(1)当m=5时,求直线AB的解析式及△AOB的面积;
(2)当y1>y2时,直接写出x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,李明和王丽家分别位于公路CD两侧的A,B处,星期天王丽要去为李明送书,他两人约定在公路CD边上见面.李明骑自行车,王丽步行,为节省时间,他们见面的地点定在距离王丽家最近的点E
(1)请你利用所学过的知识,画图确定点E的位置并写出画图依据;
(2)出门前李明发现自行车坏了,临时决定也步行前往,为节省时间,他们约定在距离他两家距离之和最小的F处见面,请你画出图形,确定点F的位置并写出画图依据.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形A1B1C1D1,黏合部分的长度为4cm.若长为30cm,宽为10cm的长方形白纸条共有100张,则小明应分配到 张长方形白纸条,才能使小明和小慧按各自要求黏合起来的长方形面积相等(要求100张长方形白纸条全部用完).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.
如:1☆3=1×32+2×1×3+1=16.
(1)求(﹣2)☆3的值;
(2)若(![]() ☆3)☆(﹣
☆3)☆(﹣![]() )=8,求a的值;
)=8,求a的值;
(3)若2☆x=m,(![]() x)☆3=n(其中x为有理数),试比较m,n的大小.
x)☆3=n(其中x为有理数),试比较m,n的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com