

·ÖĪö £Ø1£©°ŃCµć×ų±ź“śČėy=x2-2x+kæÉĘäSk=-3£¬“Ó¶ųµĆµ½Å×ĪļĻß½āĪöŹ½ĪŖy=x2-2x-3£¬Č»ŗó½ā·½³Ģx2-2x-3=0æɵƵ½A”¢BµćµÄ×ų±ź£»
£Ø2£©°Ń¶ž“ĪŗÆŹż½āĪöŹ½Åä³É¶„µćŹ½æɵĆM£Ø1£¬-4£©£¬Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚN£¬ČēĶ¼£Ø1£©£¬ĄūÓĆĖıߊĪABMCµÄĆ껿=S”÷AOC+SĢŻŠĪOCMN+S”÷MNBŗĶČż½ĒŠĪĆ껿¹«Ź½¼ĘĖć¼“æÉ£»
£Ø3£©×÷DE”ĪyÖį½»Ö±ĻßBCÓŚE£¬ČēĶ¼£Ø2£©£¬ĻČĄūÓĆ“ż¶ØĻµŹż·ØĒóµĆÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x-3£¬ÉčD£Øx£¬x2-2x-3£©£¬ŌņE£Øx£¬x-3£©£¬ŌņæɱķŹ¾³öDE=-x2+3x£¬ĄūÓĆČż½ĒŠĪĆ껿¹«Ź½µĆµ½S”÷BCD=$\frac{1}{2}$DE•3=-$\frac{3}{2}$x2+$\frac{9}{2}$x£¬Č»ŗóøł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹĒó½ā£»
£Ø4£©ĻČÅŠ¶Ļ”÷OBCĪŖµČŃüÖ±½ĒČż½ĒŠĪµĆµ½”ĻOCB=”ĻOBC=45”ć£¬ĢÖĀŪ£ŗµ±”ĻCBQ=90”揱£¬BQ½»yÖįÓŚGµć£¬ČēĶ¼£Ø3£©£¬ĖłŅŌ”ĻOBG=45”ć£¬ŌņG£Ø0£¬3£©£¬Ņ×µĆÖ±ĻßBGµÄ½āĪöŹ½ĪŖy=-x+3£¬ŌŁĶعż½ā·½³Ģ×é$\left\{\begin{array}{l}{y=-x+3}\\{y={x}^{2}-2x-3}\end{array}\right.$µĆQµć×ų±ź£»µ±”ĻBCQ=90”揱£¬CQ½»xÖįÓŚHµć£¬ČēĶ¼£Ø3£©£¬ÓĆĶ¬Ńł·½·ØµĆµ½“ĖŹ±Qµć×ų±ź£®
½ā“š ½ā£ŗ£Ø1£©°ŃC£Ø0£¬-3£©“śČėy=x2-2x+kµĆk=-3£¬
ŌņÅ×ĪļĻß½āĪöŹ½ĪŖy=x2-2x-3£¬
µ±y=0Ź±£¬x2-2x-3=0£¬½āµĆx1=-1£¬x2=3£¬ŌņA£Ø-1£¬0£©£¬B£Ø3£¬0£©£»
¹Ź“š°øĪŖ-3£¬£Ø-1£¬0£©£¬£Ø3£¬0£©£»
£Ø2£©y=x2-2x-3=£Øx-1£©2-4£¬ŌņM£Ø1£¬-4£©£¬
Å×ĪļĻߵĶŌ³ĘÖį½»xÖįÓŚN£¬ČēĶ¼£Ø1£©£¬
ĖıߊĪABMCµÄĆ껿=S”÷AOC+SĢŻŠĪOCMN+S”÷MNB=$\frac{1}{2}$”Į1”Į3+$\frac{1}{2}$”Į£Ø3+4£©”Į1+$\frac{1}{2}$”Į4”Į£Ø3-1£©=9£»
£Ø3£©“ęŌŚ£®
×÷DE”ĪyÖį½»Ö±ĻßBCÓŚE£¬ČēĶ¼£Ø2£©£¬
ÉčÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=kx+b£¬
°ŃB£Ø3£¬0£©£¬C£Ø0£¬-3£©“śČėµĆ$\left\{\begin{array}{l}{3k+b=0}\\{b=-3}\end{array}\right.$£¬½āµĆ$\left\{\begin{array}{l}{k=1}\\{b=-3}\end{array}\right.$£¬
”ąÖ±ĻßBCµÄ½āĪöŹ½ĪŖy=x-3£¬
ÉčD£Øx£¬x2-2x-3£©£¬ŌņE£Øx£¬x-3£©£¬
”ąDE=x-3-£Øx2-2x-3£©=-x2+3x£¬
”ąS”÷BCD=$\frac{1}{2}$DE•3=-$\frac{3}{2}$x2+$\frac{9}{2}$x=-$\frac{3}{2}$£Øx-$\frac{3}{2}$£©2+$\frac{27}{8}$£¬
µ±x=$\frac{3}{2}$Ź±£¬S”÷BCDÓŠ×ī“óÖµ£¬
”ßS”÷ACB=$\frac{1}{2}$”Į4”Į3=6£¬
”ąx=$\frac{3}{2}$Ź±£¬ĖıߊĪABDCµÄĆ껿×ī“ó£¬
“ĖŹ±Dµć×ų±źĪŖ£Ø$\frac{3}{2}$£¬-$\frac{15}{4}$£©£»
£Ø4£©”ßOB=OC=3£¬
”ą”÷OBCĪŖµČŃüÖ±½ĒČż½ĒŠĪ£¬
”ą”ĻOCB=”ĻOBC=45”ć£¬
µ±”ĻCBQ=90”揱£¬BQ½»yÖįÓŚGµć£¬ČēĶ¼£Ø3£©£¬Ōņ”ĻOBG=45”ć£¬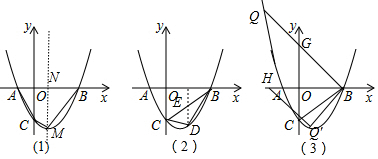
”ąOG=OB=3£¬ŌņG£Ø0£¬3£©£¬
Ņ×µĆÖ±ĻßBGµÄ½āĪöŹ½ĪŖy=-x+3£¬
½ā·½³Ģ×é$\left\{\begin{array}{l}{y=-x+3}\\{y={x}^{2}-2x-3}\end{array}\right.$µĆ$\left\{\begin{array}{l}{x=-2}\\{y=5}\end{array}\right.$»ņ$\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$£¬
”ąQ£Ø-2£¬5£©£»
µ±”ĻBCQ=90”揱£¬CQ½»xÖįÓŚHµć£¬ČēĶ¼£Ø3£©£¬Ōņ”ĻOCH=45”ć£¬
”ąOH=OC=3£¬ŌņH£Ø-3£¬0£©£¬
Ņ×µĆÖ±ĻßCHµÄ½āĪöŹ½ĪŖy=-x-3£¬
½ā·½³Ģ×é$\left\{\begin{array}{l}{y=-x-3}\\{y={x}^{2}-2x-3}\end{array}\right.$µĆ$\left\{\begin{array}{l}{x=1}\\{y=-2}\end{array}\right.$»ņ$\left\{\begin{array}{l}{x=0}\\{y=3}\end{array}\right.$£¬
”ąQ£Ø1£¬-2£©£»
×ŪÉĻĖłŹö£¬µćQ×ų±źĪŖ£Ø1£¬-2£©»ņ£Ø2£¬5£©Ź±£¬Ź¹”÷BCQŹĒŅŌBCĪŖÖ±½Ē±ßµÄÖ±½ĒČż½ĒŠĪ£®
µćĘĄ ±¾Ģāæ¼²éĮĖ¶ž“ĪŗÆŹżµÄ×ŪŗĻĢā£ŗŹģĮ·ÕĘĪÕ¶ž“ĪŗÆŹżĶ¼ĻóÉĻµćµÄ×ų±źĢŲÕ÷”¢¶ž“ĪŗÆŹżµÄŠŌÖŹ£»»įĒ󶞓ĪŗÆŹżŗĶŅ»“ĪŗÆŹżÓė×ų±źÖįµÄ½»µć×ų±ź£»ÄÜĄūÓĆĻąĖʱȱķŹ¾Ļ߶ĪÖ®¼äµÄ¹ŲĻµ£»Ąķ½ā×ų±źÓėĶ¼ŠĪŠŌÖŹ£®


 æĘѧŹµŃé»ī¶Æ²įĻµĮŠ“š°ø
æĘѧŹµŃé»ī¶Æ²įĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
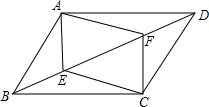 ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬ŅŃÖŖµćE”¢FŌŚ¶Ō½ĒĻß±ßBDÉĻ£¬ĒŅBE=DF£¬ĒóÖ¤£ŗĖıߊĪAECFŹĒĘ½ŠŠĖıߊĪ£®
ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬ŅŃÖŖµćE”¢FŌŚ¶Ō½ĒĻß±ßBDÉĻ£¬ĒŅBE=DF£¬ĒóÖ¤£ŗĖıߊĪAECFŹĒĘ½ŠŠĖıߊĪ£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
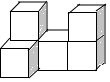 ČēĶ¼ĖłŹ¾µÄ¼øŗĪĢ壬ĘäÖ÷ŹÓĶ¼ŹĒ£Ø””””£©
ČēĶ¼ĖłŹ¾µÄ¼øŗĪĢ壬ĘäÖ÷ŹÓĶ¼ŹĒ£Ø””””£©| A£® |  | B£® | 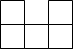 | C£® |  | D£® | 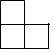 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
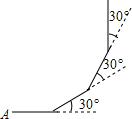 Ź®¶ž±ßŠĪµÄÄŚ½ĒŗĶŹĒ1800”ć£®
Ź®¶ž±ßŠĪµÄÄŚ½ĒŗĶŹĒ1800”ć£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com