
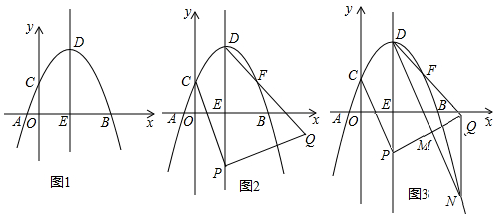
分析 (1)利用抛物线的顶点坐标的纵坐标为2即可确定出a,得出结论;
(2)设出点P的坐标.根据旋转的性质得出点Q的坐标,从而确定出直线DQ的解析式,结合抛物线解析式联立方程组即可求出点F的坐标;
(3)由(2)得出的直线PC解析式,得出直线DN解析式,结合抛物线解析式,确定出N的坐标,即可判断出QN∥DP,进而表示出NQ,DP,建立方程求解即可得出点N坐标.
解答 解:(1)∵抛物线y=ax2-2ax-a,
∴顶点坐标纵坐标为$\frac{-4{a}^{2}-4{a}^{2}}{4a}$=-2a,
∵DE=2,
∴a=-1,
∴抛物线解析式为y=-x2+2x+1,
(2)如图2,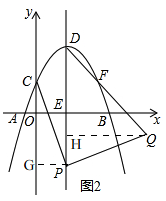
由(1)知,抛物线解析式为y=-x2+2x+1①,
∴抛物线的对称轴为x=1,D(1,2),C(0,1),
∵点P是抛物线对称轴上的动点,
∴设点P坐标为(1,t),
∴直线CP解析式为y=(t-1)x+1
过点P作PG⊥OC,过Q作QH⊥DP,
∵CP绕点P顺时针旋转90°,C的对应点为点Q,
∴QH=CG=1-t,PH=PG=1.
∴EH=1+t,
∴Q(2-t,1+t),
∵D(1,2),
∴DQ解析式为y=-x+3②,
联立①②得,$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$(舍)或$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$,
∴F(2,1);
(3)由(2)知,直线CP解析式为y=(t-1)x+1,
∵DN∥CP,D(1,2),
∴直线DN的解析式为y=(t-1)x+3-t③,
∵抛物线解析式为y=-x2+2x+1④,
联立③④得,$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$(点D的纵横坐标)或$\left\{\begin{array}{l}{x=2-t}\\{y=-{t}^{2}+2t+1}\end{array}\right.$,
∴N(2-t,-t2+2t+1),
由(2)知,Q(2-t,1+t),
∴NQ∥PD,
∴QN=(1+t)-(-t2+2t+1)=t2-t,
∵D(1,2),P(1,t),
∴DP=2-t,
∵QN=$\frac{2}{3}$DP,
∴t2-t=$\frac{2}{3}$(2-t),
∴t=$\frac{4}{3}$(此时连接DQ不能和抛物线相交,所以舍去)或t=-1,
∴N(3,-2).
点评 此题是二次函数综合题,主要考查了抛物线的顶点坐标,旋转的性质,抛物线和直线的交点坐标,解方程组,解本题的关键是确定出直线DQ的解析式和QN∥DP,是一道中等难点的中考常考题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 右边的数总是大于左边的数 | B. | 小的数,离原点近 | ||
| C. | 两个负数,较大的数离原点近 | D. | 绝对值越大的数,离原点越远 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
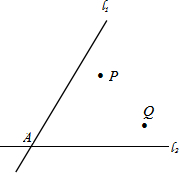 尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)
尺规作图:如图,l1、l2交于A点,P、Q的位置如图所示,试确定M点,使它到l1、l2的距离相等,且到P、Q两点的距离也相等.(保留作图痕迹)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com