
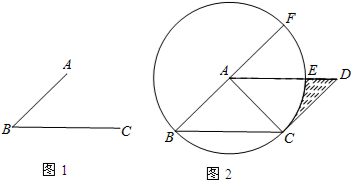
分析 (1)分别以A,C为圆心,以BC,AB的长度为半径画弧,两弧交于一点D,结论AD,CD可得;
(2)由切线的性质和平行四边形的性质得到BA⊥AC,∠ACB=∠B=45°,∠DAC=∠ACB=45°=∠FAE,根据弧长公式求出弧长,得到半径,即可求得结果.
解答  解:(1)如图所示,?ABCD即为所求;
解:(1)如图所示,?ABCD即为所求;
(2)如图2所示,∵CD与⊙A相切,
∴CD⊥AC,
在平行四边形ABCD中,
∵AB=DC,AB∥CD,AD∥BC,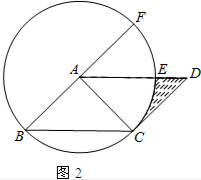
∴BA⊥AC,
∵AB=AC
∴∠ACB=∠B=45°,
∵,AD∥BC
∴∠FAE=∠B=45°,∠DAC=∠ACB=45°=∠FAE,
∴$\widehat{EF}$=$\widehat{EC}$,
∴$\widehat{EF}$的长度=$\frac{45πR}{180}$=$\frac{π}{2}$,解得R=2,
∴S阴影=S△ACD-S扇形=$\frac{1}{2}$×22-$\frac{45π{×}^{22}}{360}$=2-$\frac{π}{2}$.
点评 本题考查了基本作图,切线的性质,平行四边形的性质,弧长的求法,扇形面积的求法,知道S阴影=S△ACD-S扇形是解题的关键.


科目:初中数学 来源: 题型:选择题
 小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )
小明根据去年1~8月本班同学参加学校组织的“书香校园”活动中全班同学的课外阅读书籍的数量(单位:本),绘制了如图所示折线统计图,下列说法正确的是( )| A. | 阅读数量的平均数是57 | B. | 阅读数量的众数是42 | ||
| C. | 阅读数量的中位数是58 | D. | 有4个月的阅读数量超过60本 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | -$\frac{11}{7}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com