
【题目】有一家苗圃计划植桃树和柏树,根据市场调查与预测,种植桃树的利润![]() (万元)与投资成本x(万元)满足如图①所示的二次函数
(万元)与投资成本x(万元)满足如图①所示的二次函数![]() ;种植柏树的利润
;种植柏树的利润![]() (万元)与投资成本x(万元)满足如图②所示的正比例函数
(万元)与投资成本x(万元)满足如图②所示的正比例函数![]() =kx.
=kx.
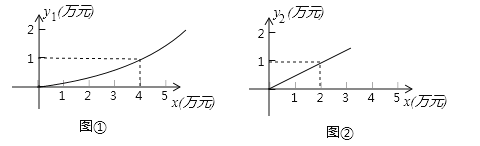
(1)分别求出利润![]() (万元)和利润
(万元)和利润![]() (万元)关于投资成本x(万元)的函数关系式;
(万元)关于投资成本x(万元)的函数关系式;
(2)如果这家苗圃以10万元资金投入种植桃树和柏树,桃树的投资成本不低于2万元且不高于8万元,苗圃至少获得多少利润?最多能获得多少利润?
【答案】(1)![]() ,
,![]() ;(2)苗圃至少获得4万元利润,最多能获得8万元利润.
;(2)苗圃至少获得4万元利润,最多能获得8万元利润.
【解析】
试题分析:(1)利用待定系数法求两个函数的解析式;
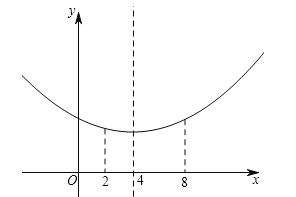
(2)根据总投资成本为10万元,设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10﹣x)万元,列函数关系式,发现是二次函数,画出函数图象,找出当2≤x≤8时的最小利润和最大利润.
试题解析:(1)把(4,1)代入![]() 中得:
中得:
16a=1,a=![]() ,∴
,∴![]() .
.
把(2,1)代入![]() =kx中得:
=kx中得:
2k=1,k=![]() ,∴
,∴![]() ;
;
(2)设种植桃树的投资成本x万元,总利润为W万元,则种植柏树的投资成本(10﹣x)万元,则W=![]() =
=![]() =
=![]() ,由图象得:当2≤x≤8时,当x=4时,W有最小值,W小=4,当x=8时,W有最大值,W大=
,由图象得:当2≤x≤8时,当x=4时,W有最小值,W小=4,当x=8时,W有最大值,W大=![]() (8﹣4)2+4=5.
(8﹣4)2+4=5.
答:苗圃至少获得4万元利润,最多能获得8万元利润.


 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】从一副普通的54张的扑克牌中随意抽出一张,有4个事件:①抽到大王;②抽到小王;③抽到2;④抽到梅花.则这4个事件发生的可能性最大的是( )
A. ① B. ② C. ③ D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
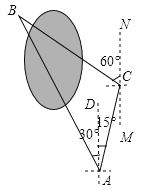
【题目】小明要测量公园北湖水隔开的两棵大树A和B之间的距离,他在A处测得大树B在A的北偏西30°方向,他从A处出发向北偏东15°方向走了200米到达C处,测得大树B在C的北偏西60°方向.
(1)求∠ABC的度数;
(2)求两棵大树A和B之间的距离(结果精确到1米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.449)
≈2.449)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(8分)

(1)把圆片沿数轴向左滚动1周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 .
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 .
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,-1,+3,-4,-3
①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com