
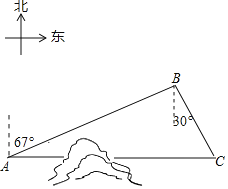
【题目】如图,C地在A地的正东方向,因有大山阻隔.由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地130km,C地位于B地南偏东30°方向.若打通穿山隧道.建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
科目:初中数学 来源: 题型:
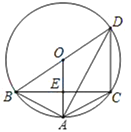
【题目】如图,△ABC内接于⊙O,∠BAC=120°,AB=AC,BD为⊙O的直径,CD=6,OA交BC于点E,
求(1)∠DBC的度数;(2)弦AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() ,
,
(1)该二次函数图象与x轴的交点坐标是______________;
(2)将![]() 化成
化成![]() 的形式_____________________,并写出顶点坐标______________.
的形式_____________________,并写出顶点坐标______________.
(3)在坐标轴中画出此抛物线的大致图象;
(4)写出不等式![]() 的解集___________________;
的解集___________________;
(5)当![]() 时,直接写出y的取值范围_________________.
时,直接写出y的取值范围_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司规定:一名客户如果一个月的通话时间不超过![]() 分钟,那么这个月这名客户只要交10元通话费;如果超过
分钟,那么这个月这名客户只要交10元通话费;如果超过![]() 分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟
分钟,那么这个月除了仍要交10元通话费外,超过部分还要按每分钟![]() 元交费.
元交费.
(Ⅰ)某名客户7月份通话90分钟,超过了规定的![]() 分钟,则超过部分应交通话费______元(用含
分钟,则超过部分应交通话费______元(用含![]() 的代数式表示);
的代数式表示);
(Ⅱ)下表表示某名客户8月份、9月份的通话情况和交费情况:
月份 | 通话时间/分钟 | 通话费总数/元 |
8月份 | 80 | 25 |
9月份 | 45 | 10 |
根据上表的数据,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() 的方程
的方程![]() .
.
(1)求证:无论![]() 取何值,这个方程总有实数根.
取何值,这个方程总有实数根.
(2)若方程的两根都是正数,求![]() 的取值范围.
的取值范围.
(3)以方程的两根为![]() 两边,斜边为
两边,斜边为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图1.已知∠ACB=∠ADB=90°,请用尺规作图作出△ABD的外接圆(保留作图痕迹,不写作法);点C是否在△ABD的外接圆上 (填“是”或“否”).
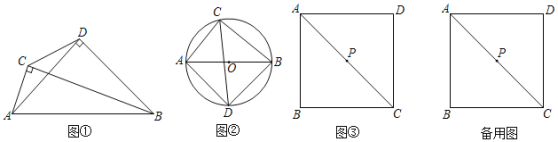
问题探究
(2)如图2.四边形ADBC是⊙O的内接四边形,∠ACB=∠ADB=90°,AD=BD.求证:CA+CB=![]() CD;
CD;
(3)如图3.点P是正方形ABCD对角线AC的中点,点E是平面上一点,EB=AB且EA=![]() BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
BA.点Q是线段AE的中点,请在图中画出点E,并求线段PQ与AB之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市射击队打算从君君、标标两名运动员中选拔一人参加省射击比赛,射击队对两人的射击技能进行了测评.在相同的条件下,两人各打靶5次,成绩统计如下:
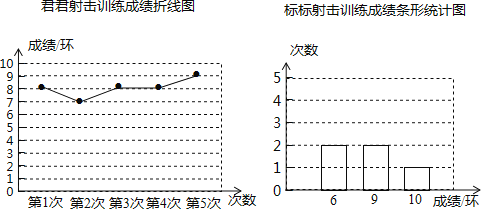
(1)填写下表:
平均数(环) | 中位数(环) | 方差(环2) | |
君君 |
| 8 | 0.4 |
标标 | 8 |
|
|
(2)根据以上信息,若选派一名队员参赛,你认为应选哪名队员,并说明理由.
(3)如果标标再射击1次,命中8环,那么他射击成绩的方差会 .(填“变大”“变小”或“不变”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】校园空地上有一面墙,长度为20m,用长为32m的篱笆和这面墙围成一个矩形花圃,如图所示.
(1)能围成面积是126m2的矩形花圃吗?若能,请举例说明;若不能,请说明理由.
(2)若篱笆再增加4m,围成的矩形花圃面积能达到170m2吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com