
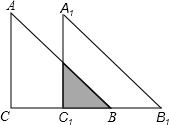
 如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,
如图,Rt△ABC中∠C=90°,AC=BC=4,将△ABC沿CB方向移动到△A1B1C1的位置,分析 (1)根据平移的性质求出BC1,再判断出重叠部分是等腰直角三角形,然后根据等腰直角三角形的面积公式列式计算即可得解;
(2)根据平移的性质求出BC1,再判断出重叠部分是等腰直角三角形,然后根据等腰直角三角形的面积公式列式计算即可得解.
解答 解:(1)由题意得,BC1=4-3=1,
∵∠C=90°,AC=BC,
∴∠ABC=45°,
∴重叠部分是等腰直角三角形,
∴重叠部分的面积=$\frac{1}{2}$×1×1=0.5;
故答案为:0.5;
(2)由题意得,BC1=4-x,
∵∠C=90°,AC=BC,
∴∠ABC=45°,
∴重叠部分是等腰直角三角形,
∴重叠部分的面积=$\frac{1}{2}$×(4-x)×(4-x)=$\frac{1}{2}$x2-4x+8.
故答案为:$\frac{1}{2}$x2-4x+8.
点评 本题考查了平移的性质,熟记性质求出BC1的长,并判断出阴影部分是等腰直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,在直角坐标系中,A(0,4),B(-3,0).
如图,在直角坐标系中,A(0,4),B(-3,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一张长为7宽为5的矩形纸片ABCD,要通过适当的剪拼,得到一个与之面积相等的正方形.
如图,有一张长为7宽为5的矩形纸片ABCD,要通过适当的剪拼,得到一个与之面积相等的正方形.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 14 | C. | 10或14 | D. | 8或10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com