
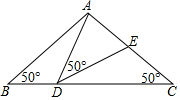
 如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.
如图,在△ABC中,AB=AC=2,∠B=∠C=50°,点D在线段BC上运动(点D不与B、C重合),连接AD,作∠ADE=50°,DE交线段AC于E.分析 (1)分两种情况进行讨论,根据三角形的外角性质,可得当∠BDA的度数为115°或100°时,△ADE的形状是等腰三角形;
(2)利用∠DEC+∠EDC=130°,∠ADB+∠EDC=130°,求出∠ADB=∠DEC,再利用AB=DC=2,即可得出△ABD≌△DCE.
解答 解:(1)∵∠B=∠C=50°,∠ADE=50°,
∴∠BDA+∠EDC=∠CED+∠EDC=130°,
∴∠BDA=∠CED,
∵点D在线段BC上运动(点D不与B、C重合),
∴AD≠AE,
ⅰ)如图所示,当EA=ED时,∠EAD=∠ADE=50°,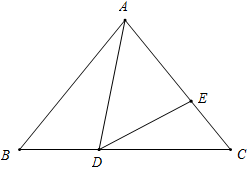
∴∠BDA=∠CED=50°+50°=100°;
ⅱ)如图所示,当DA=DE时,∠EAD=∠AED=65°,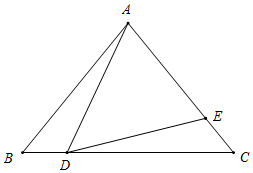
∴∠BDA=∠CED=65°+50°=115°;
(2)由(1)可得∠BDA=∠CED,
又∵∠B=∠C=50°,AB=DC=2,
∴在△ABD和△DCE中,
$\left\{\begin{array}{l}{∠BDA=∠CED}\\{∠B=∠C}\\{AB=DC}\end{array}\right.$,
∴△ABD≌△DCE(AAS).
点评 此题主要考查了等腰三角形的判定与性质,全等三角形的判定与性质,三角形外角的性质等知识点的综合应用,解决问题的关键是运用分类思想进行分类讨论.


科目:初中数学 来源: 题型:解答题
 元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:
元旦将至,某果品批发公司为指导今年的芒果销售,对往年市场销售情况进行了调查统计,得到如下数据:| 销售价x(元/千克) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(千克) | … | 2000 | 2500 | 3000 | 3500 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
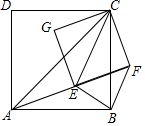 如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.
如图,已知AC、EC分别为四边形ABCD和EFCG的对角线,点E在△ABC内,∠CAE+∠CBE=90°,当四边形ABCD和EFCG均为正方形时,连接BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).
已知二次函数y=x2+bx+c的图象与直线y=x+1相交于点A(-1,m)和点B(n,5).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x | … | -3 | -2 | 1 | 2 | 3 | 4 | … |
| y | … | 12 | 5 | -4 | -3 | 0 | 5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
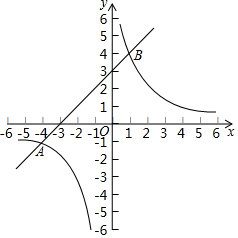 已知:如图,在平面直角坐标系xOy中,反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).
已知:如图,在平面直角坐标系xOy中,反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于点A(-4,-1)和点B(1,n).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
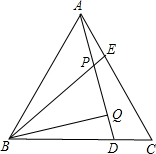 如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.
如图,已知△ABC是等边三角形,且AE=CD,AD、BE相交于P,BQ⊥AD于Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com