
分析 把点(1+$\sqrt{2}$,0)代入抛物线解析式y=2x2+kx-2求出k,再令y=0解方程即可解决.
解答 解:∵抛物线y=2x2+kx-2与x轴有一个交点坐标是(1+$\sqrt{2}$,0),
∴0=2(1+$\sqrt{2}$)2+(1+$\sqrt{2}$)k-2,
∴k=-4,
∴抛物线为y=2x2-4x-2,
令y=0则2x2-4x-2=0,
x=1$±\sqrt{2}$,
∴抛物线与x轴的另一个交点为(1-$\sqrt{2}$,0).
故答案为-4,(1-$\sqrt{2}$,0).
点评 本题考查抛物线与x轴交点问题、待定系数法等知识,解题的关键是熟练掌握待定系数法确定函数解析式,学会求抛物线与坐标轴的交点坐标,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 正方形ABCD,正方形CEFG如图放置,点B、C、E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2=$\frac{1}{2}$AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF,其中正确的是( )
正方形ABCD,正方形CEFG如图放置,点B、C、E在同一条直线上,点P在BC边上,PA=PF,且∠APF=90°,连接AF交CD于点M.有下列结论:①EC=BP;②AP=AM:③∠BAP=∠GFP;④AB2+CE2=$\frac{1}{2}$AF2;⑤S正方形ABCD+S正方形CGFE=2S△APF,其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④⑤ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如果实数a,b在数轴上如图所示,化简$\sqrt{{{(2-a)}^2}}-\sqrt{{{(a-3)}^2}}$的结果为( )
如果实数a,b在数轴上如图所示,化简$\sqrt{{{(2-a)}^2}}-\sqrt{{{(a-3)}^2}}$的结果为( )| A. | 5 | B. | 1 | C. | -2a+5 | D. | 2a-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
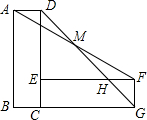 如图所示,长方形ABCD绕点C顺时针旋转90°后得到长方形CEFG,连接DG交EF于H连接AF交DG于点M,若AB=4,BC=1,则AM=$\frac{\sqrt{34}}{2}$.
如图所示,长方形ABCD绕点C顺时针旋转90°后得到长方形CEFG,连接DG交EF于H连接AF交DG于点M,若AB=4,BC=1,则AM=$\frac{\sqrt{34}}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com