
 ,1),B(s,t),C(
,1),B(s,t),C( ,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.
,0),抛物线y=x2+mx-m的顶点P是直角梯形OABC内部或边上的一个动点,m为常数.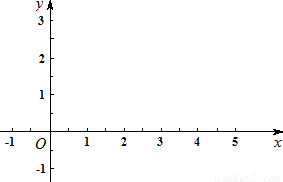
 解:
解: ,1).((1分))
,1).((1分)) ,t=1.直角梯形如图所画.(2分)
,t=1.直角梯形如图所画.(2分)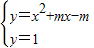 (3分)
(3分) ,不合题意,舍去.(4分)
,不合题意,舍去.(4分) ≤-m-1≤
≤-m-1≤ ,
,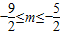 .①(5分)
.①(5分)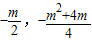 )是直角梯形OABC的内部和其边上的一个动点,
)是直角梯形OABC的内部和其边上的一个动点,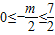 ,即-7≤m≤0. ②(6分)
,即-7≤m≤0. ②(6分)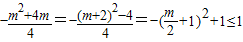 ,
,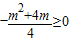 ,m(m+4)≤0,
,m(m+4)≤0,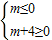 或者
或者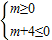 .(8分)
.(8分) x的下方,
x的下方,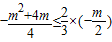 ,(10分)
,(10分)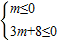 或者
或者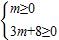 ,(*(8分)处评分后,此处不重复评分)
,(*(8分)处评分后,此处不重复评分) (11分),或m≥0 ④
(11分),或m≥0 ④ .(12分)
.(12分)

科目:初中数学 来源: 题型:
 线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.查看答案和解析>>
科目:初中数学 来源: 题型:
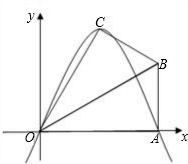
 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C,A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)在运动过程中,是否存在某一时刻t,使得以C、P、Q为顶点的三角形与△OAB相似?若存在,求出t的值;若不存在,请说明理由.
(4)将△OPQ绕着点P顺时![]() 针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
 |
查看答案和解析>>
科目:初中数学 来源:2011年江苏省无锡市积余实验学校中考数学二模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com