
| 研发组 | 管理组 | 操作组 | |
| 日工资(元/人) | 300 | 280 | 260 |
| 人数(人) | 3 | 4 | 5 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据平均数、方差、中位数和众数的定义分别对每一项进行分析,即可得出答案.
解答 解:调整前的平均数是:$\frac{300×3+280×4+260×5}{3+4+5}$=$\frac{830}{3}$(元);
调整后的平均数是:$\frac{300×4+280×2+260×6}{4+2+6}$=$\frac{830}{3}$(元),
则团队平均日工资不变,
故①错误;
调整前的方差是$\frac{1}{12}$[3(300-$\frac{830}{3}$)2+4(280-$\frac{830}{3}$)2+5(260-$\frac{830}{3}$)2]=$\frac{2300}{9}$,
调整后的方差是$\frac{1}{12}$[4(300-$\frac{830}{3}$)2+2(280-$\frac{830}{3}$)2+6(260-$\frac{830}{3}$)2]=$\frac{2900}{9}$,
则日工资的方差变大,
故②错误;
调整前:把这些数从小到大排列为:300,300,300,280,280,280,280,260,260,260,260,260,
最中间两个数的平均数是:$\frac{280+280}{2}$=280,
则中位数是280,
调整后:把这些数从小到大排列为:300,300,300,300,280,280,260,260,260,260,260,260,
最中间两个数的平均数是:$\frac{280+260}{2}$=270,
则中位数是270,
曰工资的中位数变小,
故③错误;
调整前的众数是260,调整后的众数也是260,则众数不变,
故④正确;
故选A.
点评 此题考查了平均数、方差、中位数和众数,用到的知识点:一组数据中出现次数最多的数据叫做这组数据的众数.将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.平均数是指在一组数据中所有数据之和再除以数据的个数;方差公式是S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{3600}{x}$-$\frac{3600}{2x}$=10 | B. | $\frac{3600}{2x}$-$\frac{3600}{x}$=10 | C. | $\frac{3600}{x}$+$\frac{3600}{2x}$=10 | D. | 10(2x+x)=3600 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )
如图,是某油路管道的一部分,延伸其中三条支路恰好构成一个直角三角形,其三边长分别为6cm,8cm,10cm,输油中心O在到三条支路距离相等的地方,则中心O到三条支路的管道总长(计算时视管道为线,中心O为点)为( )| A. | 24cm | B. | 12cm | C. | 10cm | D. | 6cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
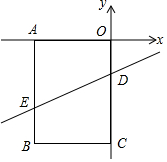 如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).
如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(-2,-3),直线y=$\frac{1}{2}$x-1与OC、AB分别交于占D、E,点P在矩形的边AB或BC上,作PF⊥ED于点F,连接PD,当△PFD是等腰三角形时,点P的坐标为(-$\frac{2}{3}$,-3)或(-2,-$\frac{1}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=-3x+3与x轴、y轴分别父于A、B两点,点A关于直线x=-1的对称点为点C.
直线y=-3x+3与x轴、y轴分别父于A、B两点,点A关于直线x=-1的对称点为点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com