
【题目】“六一”儿童节,某玩具超市设立了一个如图所示的可以自由转动的转盘,开展有奖购买活动.顾客购买玩具就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应奖品.下表是该活动的一组统计数据.下列说法不正确的是( )

转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“铅笔”区域的次数m | 68 | 108 | 140 | 355 | 560 | 690 |
落在“铅笔”区域的频率 | 0.68 | 0.72 | 0.70 | 0.71 | 0.70 | 0.69 |
A. 当n很大时,估计指针落在“铅笔”区域的频率大约是0.70
B. 假如你去转动转盘一次,获得铅笔的概率大约是0.70
C. 如果转动转盘2000次,指针落在“文具盒”区域的次数大约有600次
D. 转动转盘10次,一定有3次获得文具盒
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.a3·(-a2)= a5
B.(-ax 2)3=-a x6
C.3x3-x(3x2-x+1)=x2-x
D.(x+1)(x-3)=x2+x-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若(x+m)(x+n)=x2 -6x+5,则( )
A.m , n同时为负
B.m , n同时为正
C.m , n异 号
D.m , n异号且绝对值小 的为正
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知BD是矩形ABCD的对角线.

(1)用直尺和圆规作线段BD的垂直平分线,分别交AD、BC于E、F(保留作图痕迹,不写作法和证明).
(2)连结BE,DF,问四边形BEDF是什么四边形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
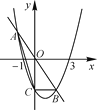
【题目】已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
(1)写出点C的坐标并求出此抛物线的解析式;
(2)当原点O为线段AB的中点时,求k的值及A,B两点的坐标;
(3)是否存在实数k使得△ABC的面积为![]() ?若存在,求出k的值;若不存在,请说明理由.
?若存在,求出k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为800元,出售标价为1200元,后来由于该商品积压,商店准备打折销售,要保证利润率不低于5%,该商品最多可打 ( )
A. 9折B. 8折C. 7折D. 6折
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】操作与探究:
(1)对数轴上的点P进行如下操作:先把点P表示的数乘以![]() ,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
,再把所得数对应的点向右平移1个单位,得到点P的对应点P′.
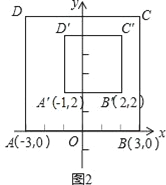
点A,B在数轴上,对线段AB上的每个点进行上述操作后得到线段A′B′,其中点A,B的对应点分别为A′,B′.如图1,若点A表示的数是﹣3,则点A′表示的数是 ;若点B′表示的数是2,则点B表示的数是 ;已知线段AB上的点E经过上述操作后得到的对应点E′与点E重合,则点E表示的数是 .

(2)如图2,在平面直角坐标系xOy中,对正方形ABCD及其内部的每个点进行如下操作:把每个点的横、纵坐标都乘以同一个实数a,将得到的点先向右平移m个单位,再向上平移n个单位(m>0,n>0),得到正方形A′B′C′D′及其内部的点,其中点A,B的对应点分别为A′,B′.已知正方形ABCD内部的一个点F经过上述操作后得到的对应点F′与点F重合,求点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
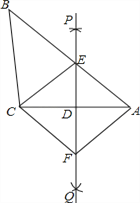
【题目】如图,在△ABC中, PQ是CA的垂直平分线, CF∥AB交PQ于点F,连接AF.
(1)求证:△AED≌△CFD;
(2)求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)![]()
(2)20132﹣2012×2014(简便计算)
(3)(3a2)3+a2a4﹣a8÷a2
(4)(x﹣2)(3x﹣1)
(5)(x﹣1)(x+1)﹣(x+2)2
(6)(a+3b﹣2c)(a﹣3b﹣2c)
(7)(m﹣2n+1)2
(8)(2a﹣3b)2(2a+3b)2 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com