
 如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.
如图,正方形ABCO的边OA、OC在坐标轴上,点B坐标为(6,6),将正方形ABCO绕点C逆时针旋转角度α(0°<α<90°),得到正方形CDEF,ED交线段AB于点G,ED的延长线交线段OA于点H,连CH、CG.分析 (1)根据旋转变换的性质得到DC=CO,∠CDG=∠COA=90°,根据正方形的性质得到CB=CO,∠B=90°,根据直角三角形的全等的判定定理证明即可;
(2)证明Rt△COH≌Rt△CDH,得到∠OCH=∠DCH,HO=DH,等量代换即可;
(3)根据矩形的判定定理证明四边形AEBD是矩形,设点H的坐标为(x,0),根据勾股定理列出方程,解方程求出x的值,得到点H的坐标.
解答 解(1)∵将正方形ABCO绕点C逆时针旋转角度α,
∴DC=CO,∠CDG=∠COA=90°,
∵四边形OCBA是正方形,
∴CB=CO,∠B=90°,
∴CB=CD,∠B=∠CDG=90°
在Rt△CDG与Rt△CBG中,
$\left\{\begin{array}{l}{CD=CB}\\{CG=CG}\end{array}\right.$,
∴Rt△CDG≌Rt△CBG;
(2)∵∠CDG=90°,
∴∠CDH=90°,
在Rt△COH与Rt△CDH中,
$\left\{\begin{array}{l}{CO=CD}\\{CH=CH}\end{array}\right.$,
∴Rt△COH≌Rt△CDH,
∴∠OCH=∠DCH,HO=DH,
∵Rt△CDG≌Rt△CBG,
∴∠DCG=∠BCG,DG=BG,
∴∠HCG=∠DCG+∠DCH=45°,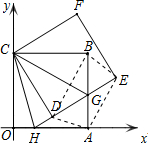
HG=HD+DG=HO+BG;
(3)当G是AB中点时,四边形ADBE是矩形,
∵G是AB中点,
∴BG=AG=$\frac{1}{2}$AB
由(2)得DG=BG,
又∵AB=DE,
∴DG=$\frac{1}{2}$DE,
∴DG=GE=BG=AG,
∴四边形AEBD是平行四边形,
∵AB=DE,
∴□ADBE是矩形,
设点H的坐标为(x,0),
则HO=HD=x,DG=BG=AG=3,AH=6-x,
由勾股定理得,(6-x)2+33=(3+x)2,
解得,x=2,
∴H(2,0).
点评 本题考查的是正方形的性质、旋转变换的性质、全等三角形的判定和性质,掌握旋转变换的性质、正方形的四条边相等、四个角都是90°是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=2,b=-1 | B. | a=-4,b=3 | C. | a=1,b=-7 | D. | a=-7,b=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{\begin{array}{l}{4x>x-9}\\{\frac{1+3x}{2}>2x}\end{array}\right.$,并把解集在数轴上表示出来.
解不等式组:$\left\{\begin{array}{l}{4x>x-9}\\{\frac{1+3x}{2}>2x}\end{array}\right.$,并把解集在数轴上表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com