
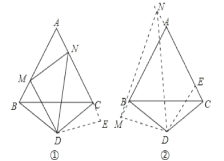
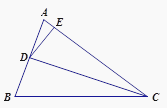
【题目】如图①,△ABC是正三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角,角两边分别交AB,AC边于M,N两点,连接MN.

(1)探究:线段BM,MN,NC之间的关系,并加以证明。
(2)若点M是AB的延长线上的一点,N是CA的延长线上的点,其它条件不变,请你再探线段BM,MN,NC之间的关系,在图②中画出图形,并说明理由。
【答案】(1)MN=BM+NC.理由见解析;(2)MN=NCBM,图见解析,理由见解析;
【解析】
(1)延长AC至E,使得CE=BM并连接DE,构造全等三角形,找到相等的线段,MD=DE,再进一步证明△DMN≌△DEN,进而得到MN=BM+NC.
(2)按要求作出图形,先证△BMD≌△CED,再证△MDN≌△EDN(SAS),即可得出结论.
(1)MN=BM+NC.理由如下:
延长AC至E,使得CE=BM(或延长AB至E,使得BE=CN),并连接DE.
∵△BDC为等腰三角形,△ABC为等边三角形,
∴BD=CD,∠DBC=∠DCB,∠MBC=∠ACB=60°,
又BD=DC,且∠BDC=120°,
∴∠DBC=∠DCB=30°,
∴∠ABC+∠DBC=∠ACB+∠DCB=60°+30°=90°,
∴∠MBD=∠ECD=90°,
在△MBD与△ECD中,
∵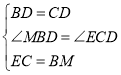 ,
,
∴△MBD≌△ECD(SAS),
∴MD=DE,
∴△DMN≌△DEN,
∴MN=BM+NC.
(2)按要求作出图形,(1)中结论不成立,应为MN=NCBM.
在CA上截取CE=BM.
∵△ABC是正三角形,
∴∠ACB=∠ABC=60°,
又∵BD=CD,∠BDC=120°,
∴∠BCD=∠CBD=30°,
∴∠MBD=∠DCE=90°,
在△BMD和△CED中
∵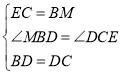 ,
,
∴△BMD≌△CED(SAS),
∴DE=DM,
在△MDN和△EDN中
∵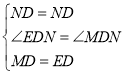 ,
,
∴△MDN≌△EDN(SAS),
∴MN=NE=NCCE=NCBM.


 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知CD是△ABC中∠ACB的角平分线,E是AC上的一点,且CD2=BC·CE,AD=6,AE=4.
(1)求证:△BCD∽△DCE;
(2)求证:△ADE∽△ACD;
(3)求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
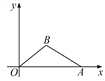
【题目】如图,在直角坐标系内,O为原点,点A的坐标为(10,0),点B在第一象限内,BO=5,sin∠BOA=![]() . 求:(1)点B的坐标;(2)cos∠BAO的值.
. 求:(1)点B的坐标;(2)cos∠BAO的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC在坐标平面内,三个顶点的坐标为A(0,3)、B(3,4)、C(2,2),(正方形网格中,每个小正方形边长为1个单位长度)
(1)画出△ABC向下平移4个单位得到的△A1B1C1;
(2)以B为位似中心,在网格中画出△A2BC2,使△A2BC2与△ABC位似,且位似比2∶1,直接写出C2点坐标是 ;
(3)△A2BC2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
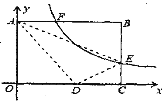
【题目】如图,将矩形ABCO放在直角坐标系中,其中顶点B的坐标为(10, 8),E是BC边上一点将△ABE沿AE折叠,点B刚好与OC边上点D重合,过点E的反比例函数y=![]() 的图象与边AB交于点F, 则线段AF的长为( )
的图象与边AB交于点F, 则线段AF的长为( )
A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解2018年全国中学生数学竞赛情况,随机抽查了部分参赛同学的成绩,整理并制作图表如下(部分未完成).请根据以上图表中提供的信息,解答下列问题:
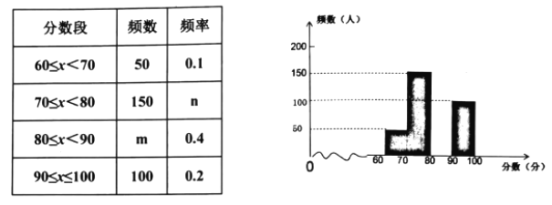
(1)本次调查的样本容量为______________.
(2)在表中:m=_____________,n=____________.
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,某中学有200人参加比赛,那么你估计该校约有多少人取得优秀成绩?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(![]() )如图
)如图![]() ,
, ![]() 是
是![]() 形内的高,
形内的高, ![]() 是
是![]() 的外接圆⊙
的外接圆⊙![]() 的直径.
的直径.
①求证: ![]() .
.
②若![]() ,
, ![]() ,
, ![]() ,⊙
,⊙ ![]() 的直径
的直径![]() 长.
长.
③如图,在边长为![]() 的小正方形组成的网格之中有一个格点三角形
的小正方形组成的网格之中有一个格点三角形![]() ,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
,请你从上面两小题中获得经验,直接写出此格点三角形的外接圆面积.
(![]() )如图
)如图![]() ,
, ![]() 是
是![]() 形外的高,若
形外的高,若![]() ,
, ![]() ,
, ![]() ,(
,( ![]() )题中②的结论是否还成立?成立与否都要说明理由.
)题中②的结论是否还成立?成立与否都要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一块直角三角形绿地,两直角边长分别为3m,4m,现在要将绿地扩充成等腰三角形,且扩充时只能延长长为3m的直角边,则扩充后等腰三角形绿地的面积为____m2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com