
| 2 |
| 2 |
|
|
| -1±p |
| 2 |
| a+b | ||
|
| a-b | ||
|


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:阅读理解
| 1 |
| 2 |
| 1 |
| 2 |


查看答案和解析>>
科目:初中数学 来源: 题型:
 顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.
顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
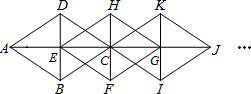 顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.
顶点,如菱形ABCD、EFGH、CIJK…,要求每个菱形的两条对角线长分别为4m和6m.查看答案和解析>>
科目:初中数学 来源:2010年浙江省宁波市慈溪中学保送生招生考试数学模拟试卷(三)(解析版) 题型:解答题
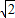 ,同时求其差再除以
,同时求其差再除以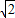 ,加上剩下的一个数,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,得到2004,2005,2006?证明你的结论.
,加上剩下的一个数,这样就仍得到三个数.再对所得三个数进行如上操作,问能否经过若干次上述操作,得到2004,2005,2006?证明你的结论.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com