
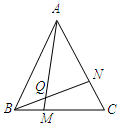 ��1��ѧ��ȫ���������Ժ���ʦ����������һ���⣺��ͼ����M��N�ֱ��ڵȱߡ�ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q����֤����BQM=60�㣮��ע�⣺�ȱ������������߶���ȣ�ÿ���ڽǶ���60�㣩
��1��ѧ��ȫ���������Ժ���ʦ����������һ���⣺��ͼ����M��N�ֱ��ڵȱߡ�ABC��BC��CA���ϣ���BM=CN��AM��BN���ڵ�Q����֤����BQM=60�㣮��ע�⣺�ȱ������������߶���ȣ�ÿ���ڽǶ���60�㣩���� ��1���ɡ�ABCΪ�ȱ������Σ����õȱ������ε����ʵõ���������ȣ���������ȣ�����SAS�õ���ABM���BCNȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�һ�Խ���ȣ�����������ʼ������������ɵ�֤��
��2�����������⣬��������۽��������������Խ���ȵ����������Ƶõ���BMQ���ABM���ƣ��������������εĶ�Ӧ����ȵõ�һ�Խ���ȣ�����ASA�õ���ABM���BCNȫ�ȣ�����ȫ�������ζ�Ӧ����ȼ��ɵ�֤�����������⣬������ǵ����ʵõ��н���ȣ�����SAS�õ���ACM���ABNȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�һ�Խ���ȣ����õ�ʽ�����ʱ��μ��ɵ�֤��
���  �⣺��1����ͼ1���ߡ�ABCΪ�ȱ������Σ�
�⣺��1����ͼ1���ߡ�ABCΪ�ȱ������Σ�
��AB=BC=AC����BAC=��ABC=��ACB=60�㣬
�ڡ�ABM�͡�BCN�У�
$\left\{\begin{array}{l}{BM=CN}\\{��ABM=��BCN}\\{AB=BC}\end{array}\right.$��
���ABM�ա�BCN��SAS����
���BAM=��CBN��
���BQM=��BAQ+��ABQ=��MBQ+��ABQ=60�㣻
��2�����ǣ����ǣ�
��ѡ��٣���֪����ͼ1����BQM=60�㣬
��֤��BM=CN��
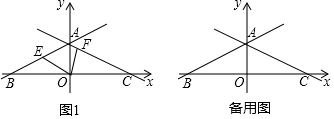
֤�����ߡ�BQM=��ABM=60�㣬��BMQ=��AMB��
���BMQ�ס�AMB��
���CBN=��BAM��
�ڡ�ABM�͡�BCN�У�
$\left\{\begin{array}{l}{��BAM=��CBN}\\{AB=BC}\\{��ABM=��BCN}\end{array}\right.$��
���ABM�ա�BCN��ASA����
��BM=CN��
��ѡ��ڣ���֪����ͼ2����M��N�ֱ��ڵȱߡ�ABC��BC��CA�ߵ��ӳ����ϣ���BM=CN��AM��BN���ڵ�Q��
��֤����BQM=60�㣮
֤������ͼ2����BM=CN��BC=BQ����ACB=��BAC=60�㣬
��CM=AN����ACM=��BAN=120�㣬
�ڡ�ACM�͡�BAN�У�
$\left\{\begin{array}{l}{CM=AN}\\{��ACM=��BAN}\\{AC=BA}\end{array}\right.$��
���ACM�ա�BAN��SAS����
���M=��N��
���NQA=��NBC+��M=��NBC+��N=180��-��ACB=120�㣬
���BQM=60�㣮
���� ���⿼����ȫ�������ε��ж������ʡ��ȱ������ε����ʡ��������ڽǺͶ����Լ���������ǵ����ʵ����ã���������ȫ�������ε��ж��������ǽⱾ��Ĺؼ�������ʱע�⣺ȫ�������ζ�Ӧ����ȣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����E��������ABCD�ڣ�AE=6��BE=8��AB=10��
��ͼ����E��������ABCD�ڣ�AE=6��BE=8��AB=10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com