
分析 (1)根据题意画出树状图,再根据甲、乙两人出第一次手势时,共有9种等可能的结果数,其中出现相同手势的结果数为3,于是根据概率公式可计算出不分胜负的概率;
(2)根据题意得出所有27种等可能的结果数,再找出三种手势都相同或都不相同的结果数,然后根据概率公式求解即可.
解答 解:(1)根据题意画图如下: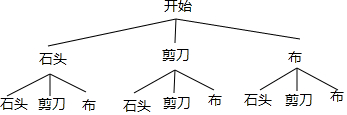
甲、乙两人出第一次手势时,共有9种等可能的结果数,其中出现相同手势的结果数为3,
则一次游戏中甲、乙两人出第一次手势时,不分胜负的概率$\frac{3}{9}$=$\frac{1}{3}$;
(2)∵游戏中甲、乙、丙三人出第一次手势时,共有27种等可能的结果数,其中三种手势都相同或都不相同的结果数为9,
∴甲、乙、丙三人出第一次手势时,不分胜负的概率$\frac{9}{27}$=$\frac{1}{3}$;
点评 本题考查了列表法或树状图法:通过列表法或树状图法展示所有等可能的结果求出n,再从中选出符合事件A或B的结果数目m,然后根据概率公式求出事件A或B的概率.


 精英口算卡系列答案
精英口算卡系列答案科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.
如图,在△ABC中,已知AB=AC=10$\sqrt{2}$cm,∠BAC=90°,点D在AB边上且BD=4cm,过点D作DE⊥AB交BC于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com