
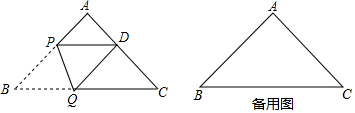
分析 (1)由折叠得出PQ是AB的垂直平分线,进而得出PQ是△ABC的中位线,即可得出结论;
(2)①由折叠得出PD=BP=4-y,再用勾股定理建立方程即可得出结论;
②根据等腰三角形的定义,分①PD=DQ时,BP=BQ,再根据翻折变换前后的线段相等判断出BP=BQ=PD=DQ,从而得到四边形BQDP是菱形,根据菱形的对边平行可得PD∥BC,BP∥DQ,然后判断出△APD和△CDQ都是等腰直角三角形,根据等腰直角三角形的性质用AD表示出PD、CD,然后根据AC的长度列方程求解即可;②DQ=PQ时,BQ=PQ,求出△BPQ是等腰直角三角形,点B与点C重合,从而得到AD=AC;③PD=PQ时,PQ=BP,然后求出△BPQ是等腰直角三角形,点B与点A重合,不符合题意.
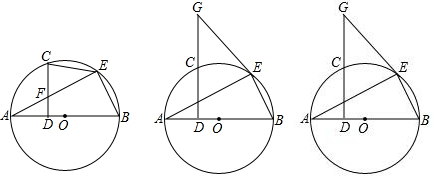
解答 解:(1)如图,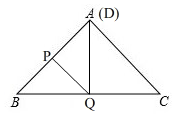
当点D和点A重合时,
由折叠知,AP=BP,∠BPQ=∠APQ,
∵∠APQ+∠BPQ=180°,
∴∠BPQ=∠APQ=90°=∠BAC,
∴PQ∥AC,
∵AP=BP,
∴PQ是△ABC的中位线,
∴PQ=$\frac{1}{2}$AC=2;
(2)∵AD=x,AC=4,
∴CD=4-x,
∵AP=y,AB=4,
∴BP=4-y,
在△ABC中,∠BAC=90°,AC=AB=4,
∴BC=4$\sqrt{2}$,∠B=∠C=45°,
如图1,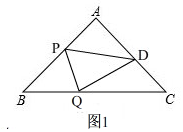
由折叠知,DP=BP=4-y,
在Rt△ADP中,根据勾股定理得,AP2+AD2=PD2,
∴y2+x2=(4-y)2,
∴y=-$\frac{1}{8}$x2+2(0≤x≤4);
(3)①PD=DQ时,BP=BQ,
由翻折变换得,BP=PD,BQ=DQ,
∴BP=BQ=PD=DQ,
∴四边形BQDP是菱形,
∴PD∥BC,BP∥DQ,
∵∠A=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴△APD和△CDQ都是等腰直角三角形,
在Rt△APD中,PD=$\sqrt{2}$AD=$\sqrt{2}$x,
在Rt△CDQ中,CD=DQ,
∵PD=DQ,
∴CD=$\sqrt{2}$AD,
∵AC=AD+CD,
∴AD+$\sqrt{2}$AD=4,
即:x+$\sqrt{2}$x=4
解得AD=4$\sqrt{2}$-4;
②DQ=PQ时,BQ=PQ,
∴∠BPQ=∠B=45°,
∴△BPQ是等腰直角三角形,
∴点B与点C重合,
∴x=AD=AC=4;
③PD=PQ时,PQ=BP,
∴∠BQP=∠B=45°,
∴△BPQ是等腰直角三角形,
∴点B与点A重合,
此时,点B与点A重合,不符合题意,舍去;
综上所述,AD的长度为4或4$\sqrt{2}$-4.
点评 此题是几何变换综合题,主要考查了等腰直角三角形的性质,折叠的性质,三角形的中位线定理,勾股定理,等腰三角形的性质,解(1)的关键是得出PQ是AB的垂直平分线,解(2)①的关键是利用勾股定理建立方程,解(2)②的关键是分类讨论思想,是一道中考常考题.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源:2016~2017学年安徽省芜湖市九年级下学期第一次模拟考试数学试卷(解析版) 题型:解答题
在一个不透明的袋子中装有除颜色外其余均相同的5个小球,其中红球3个(记为A1,A2,A3),黑球2个(记为B1,B2).
(1)若先从袋中取出m(m>0)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,填空:①若A为必然事件,则m的值为 ②若A为随机事件,则m的取值为
(2)若从袋中随机摸出2个球,正好红球、黑球各1个,用树状图或列表法求这个事件的概率.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年贵州省七年级下学期第一次月考数学试卷(解析版) 题型:单选题
已知下列命题:①相等的角是对顶角;②邻补角的平分线相互垂直;③互补的两个角一定是一个锐角,另一个为钝角;④平行于同一条直线的两个直线平行.其中真命题的个数是( )
A.  个 B.
个 B. 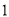 个 C.
个 C. 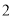 个 D.
个 D. 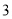 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
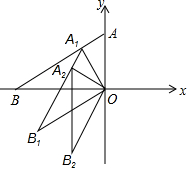 如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )
如图,点A(0,1),点B(-$\sqrt{3}$,0),作OA1⊥AB,垂足为A1,以OA1为边作Rt△A1OB1,使∠A1OB1=90°,∠B1=30°,作OA2⊥A1B1,垂足为A2,再以OA2为边作Rt△A2OB2,使∠A2OB2=90°,∠B2=30°,…,以同样的作法可得到Rt△AnOBn,则当n=2017时,点A2017的纵坐标为( )| A. | ($\frac{\sqrt{3}}{2}$)2017 | B. | -($\frac{\sqrt{3}}{2}$)2017 | C. | ($\frac{\sqrt{3}}{2}$)2018 | D. | -($\frac{\sqrt{3}}{2}$)2018 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
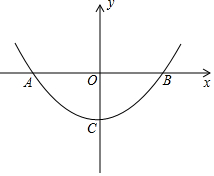 抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).
抛物线y=ax2+c与x轴交于A、B两点,顶点为C,点P在抛物线上,P(1,-3),B(4,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com