
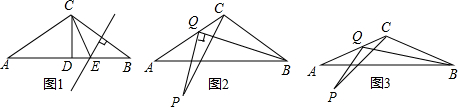
分析 (1)根据等腰三角形的性质得到AD=BD=$\frac{1}{2}$AB=4,由勾股定理得到CD=3,由线段垂直平分线的性质得到CE=BE,根据勾股定理即可得到结论;
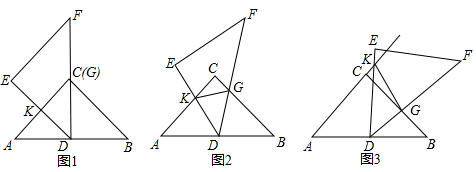
(2)如图2,过C作CD⊥CQ交BQ于D,根据等腰三角形的性质得到∠ACB=120°,根据角平分线的定义得到∠CBQ=15°,推出△CQD是等腰直角三角形,求得DQ=$\sqrt{2}$CQ,根据全等三角形的性质得到BD=PQ,于是得到结论;
(3)如图3,作∠QCD=120°交BQ于D,过C作CH⊥BQ于H,根据角的和差得到∠QCP=∠BCD,根据等腰三角形的性质得到∠ACB=140°,根据全等三角形的性质得到BD=PQ,于是得到结论.
解答 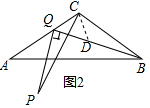 解:(1)∵AC=BC=5,CD⊥AB,
解:(1)∵AC=BC=5,CD⊥AB,
∴AD=BD=$\frac{1}{2}$AB=4,
∴CD=3,
∵BC的垂直平分线交AB于E,
∴CE=BE,
∴DE=4-BE,
∵CD2+DE2=CE2,
∴32+(4-BE)2=BE2,
∴BE=$\frac{25}{8}$;
(2)如图2,过C作CD⊥CQ交BQ于D,
∵AC=BC,∠ABC=30°,
∴∠ACB=120°,
∵BQ平分∠ABC,
∴∠CBQ=15°,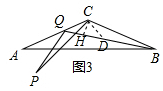
∴∠CQB=45°,
∴△CQD是等腰直角三角形,
∴DQ=$\sqrt{2}$CQ,
∵∠PQB=∠BCP=90°,
∴∠P=∠CBQ=15°,
在△CQP与△CDB中,$\left\{\begin{array}{l}{∠P=∠CBE}\\{∠PQC=∠BDC=135°}\\{CQ=CD}\end{array}\right.$,
∴△CQP≌△CDB,
∴BD=PQ,
∵BQ=BD+DQ,
∴BQ=PQ+$\sqrt{2}$CQ;
(3)如图3,作∠QCD=120°交BQ于D,过C作CH⊥BQ于H,
∵∠PCB=∠PQB=120°,
∴∠QCP=∠BCD,
∵AC=BC,∠ABC=20°,
∴∠ACB=140°,
∵BQ平分∠ABC,
∴∠CBQ=10°,
∴∠CQB=30°,
∴∠CDQ=30°,
∴CQ=CD,
∴DQ=2QH=$\sqrt{3}$CQ,
在△CQP与△CDB中,$\left\{\begin{array}{l}{∠QCP=∠DCB}\\{CQ=CD}\\{∠PQC=∠BDC=150°}\end{array}\right.$,
∴△CQP≌△CDB,
∴BD=PQ,
∵BQ=BD+DQ,
∴BQ=PQ+$\sqrt{3}$CQ.
点评 本题考查了全等三角形的判断和性质,等腰三角形的判定和性质,角平分线的定义,等腰直角三角形的判定和性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
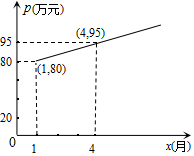 在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活成为人们的共识,某企业采用技术革新,节能减排,经分析前5个月二氧化碳排放量y(吨)与月份x(月)之间的函数关系是y=-2x+50.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
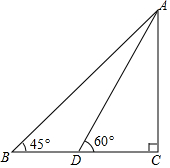 如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)
如图,某滑雪运动员训练时的斜坡示意图,某次训练拟将难度系数加大,决定将训练的斜坡的倾角由45°升为60°,已知原斜坡AB的长为3$\sqrt{6}$米,点B、D、C在同一水平地面上.若斜坡的正前方能有6米长的空地就能保证安全,已知原斜坡屈的前方有3米长的空地,进行这样的改造是否可行?并说明理由.(参考数据:$\sqrt{3}$=1.732,$\sqrt{6}$=2.449)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
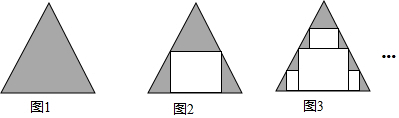
| A. | $\frac{\sqrt{3}}{{2}^{n-1}}{a}^{2}$ | B. | $\frac{\sqrt{3}}{{2}^{n}}{a}^{2}$ | C. | $\frac{\sqrt{3}}{{2}^{n+1}}{a}^{2}$ | D. | $\frac{\sqrt{3}}{{2}^{n+2}}{a}^{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com