Question

如果一个点能与另外两个点构成直角三角形，则称这个点为另外两个点的勾股点．例如：矩形ABCD中，点C与A，B两点可构成直角三角形ABC，则称点C为A，B两点的勾股点．同样，点D也是A，B两点的勾股点

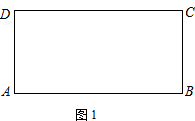
1.如图1，矩形ABCD中，AB＝3，BC＝1，请在边CD上作出A，B两点（除C,D以外）的勾股点（要求：尺规作图，保留作图痕迹，不要求写作法）．

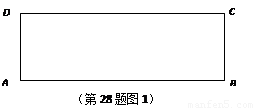
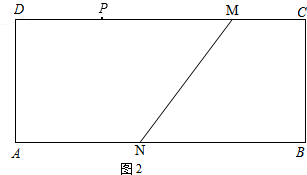
（1）       2.如图2，矩形ABCD中，

AB＝12cm，BC＝4 cm，DM＝8 cm，AN＝5 cm．动点P从D点出发沿着DC方向以1 cm／s的速度向右移动，过点P的直线l平行于BC，当点P运动到点M时停止运动．设运动时间为t(s) ，点H为M，N两点的勾股点，且点H在直线l上．

①当t＝4，求PH的长．

②探究满足条件的点H的个数（直接写出点H的个数及相应t的取值范围，不必证明）．

 

Answer 1

【答案】

 

1.以线段AB为直径的圆与线段CD的交点有两个  ----------1分

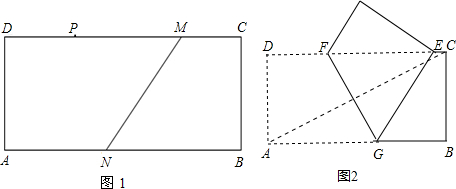
2.①当t＝4时，有3个勾股点.如图，

 

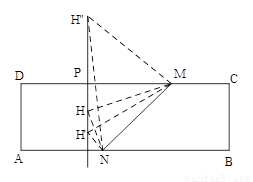
PH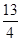＝或PH＝2或PH＝3 ．每种情况各1分 --3分

②当0≤ t＜4时，有2个勾股点；

  当t＝4时，有3个勾股点；

当4＜t＜5时，有4个勾股点；

当t＝5时，有2个勾股点；

当5＜t＜8时，有4个勾股点；

当t＝8时，有2个勾股点．       -------------------------5分

（除①的情况，其余每种1分）

综上所述，当0≤ t＜4或t＝5或t＝8时，有2个勾股点；当t＝4时，有3个勾股点；当4＜t＜5或5＜t＜8时，有4个勾股点．

【解析】（1）以线段AB为直径的圆与线段CD的交点，或线段CD的中点就是A，B两点在CD上的勾股点；

（2）①如图，当t=4时，PM=8-4=4，QN=5-4=1，分三种情况：

当∠MHN=90°时，根据已知条件可以证明△PMH∽△QHN，然后利用相似三角形对应线段成比例即可求出PH；

当∠H''NM=90°时，设PH=x，那么H''Q=4-x，根据勾股定理得到PM²+PH''²=QN²+H''Q²+MN²，而MN=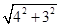=5，依次即可求出PH''；

当∠H'MN=90°时，根据勾股定理得到H'P²+PM²+QH'²+QN²=MN²，而H'Q=PH'+PQ=PH'+4，依次即可求出PH'．

②利用①的结果可以探究满足条件的点H的个数及相应t的取值范围．