
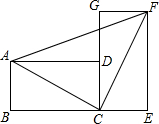
 把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为
把两个全等的矩形ABCD和矩形CEFG拼成如图所示的图案,若BC=4,AB=2,则△ACF的面积为| AB2+BC2 |
| 22+42 |
| 20 |
|
| 20 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
|
|
| A、m-16n=5 |
| B、m-16n=11 |
| C、m+16n=-11 |
| D、m+16n=-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
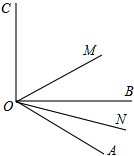 如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.
如图,已知∠AOC与∠AOB的和为180度,OM,ON分别是∠AOC、∠AOB的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:
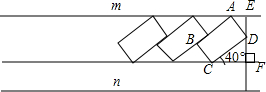 某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.
某住宅小区的物业管理部门为解决部门为解决住户停车困难问题,将一条道路开辟为停车场,停车位置如图所示,已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4m,BC=2.2m,∠DCF=40°.请计算停车位所占道路的宽度EF.(结果精确到0.1m)参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84.| A、8.6 | B、5.2 |
| C、4.8 | D、5.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com