练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，AB⊥BC，DC⊥BC，若∠DBC=45°，∠A=70°，求∠D，∠AED，∠BFE的度数．

    【答案】∠D=45°；∠AED=70°；∠BFE=115°．

    【解析】

    根据直角三角形两锐角互余列式求解即可得到∠D，根据在同一平面内垂直于同一直线的两直线互相平行可得AB∥CD，再根据两直线平行，内错角相等可得∠AED=∠A，然后根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFE=∠D+∠AED．

    ∵DC⊥BC，∠DBC=45°，∴∠D=90°﹣∠DBC=90°﹣45°=45°；

    ∵AB⊥BC，DC⊥BC，∴AB∥DC，∴∠AED=∠A=70°；

    在△DEF中，∠BFE=∠D+∠AED=45°+70°=115°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】为发展校园足球运动，某县城区四校决定联合购买一批足球运动装备，市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球队服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

    （1）求每套队服和每个足球的价格是多少？

    （2）若城区四校联合购买100套队服和a个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用；

    （3）假如你是本次购买任务的负责人，你认为到哪家商场购买比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】计算：

    (1)(－3pq)2；

    (2)－x3＋(－4x)2x；

    (3)(m4m÷m2n)·mn；

    (4)(－2)－2－32÷(3.144＋π)0；

    (5)(a2)3·(a2)4÷(－a2)5；

    (6)[－2－3－8－1×(－1)－2]×.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CA⊥AB，DB⊥AB，已知AC=2，AB=6，点P射线BD上一动点，以CP为直径作⊙O，点P运动时，若⊙O与线段AB有公共点，则BP最大值为　 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，BE是圆O的直径，A在EB的延长线上，AP为圆O的切线，P为切点，弦PD垂直于BE于点C．
    （1）求证：∠AOD=∠APC；
    （2）若OC：CB=1：2，AB=6，求圆O的半径及tan∠APB．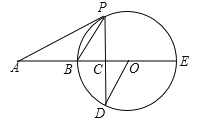

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，学校大门出口处有一自动感应栏杆，点A是栏杆转动的支点，当车辆经过时，栏杆AE会自动升起，某天早上，栏杆发生故障，在某个位置突然卡住，这时测得栏杆升起的角度∠BAE=127°，已知AB⊥BC，支架AB高1.2米，大门BC打开的宽度为2米，以下哪辆车可以通过？（　　）
    （栏杆宽度，汽车反光镜忽略不计）
    （参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75．车辆尺寸：长×宽×高）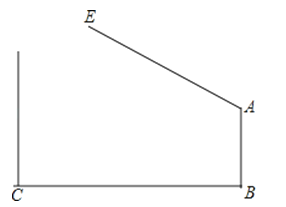

    A.宝马Z4（4200mm×1800mm×1360mm）
    B.奇瑞QQ（4000mm×1600mm×1520mm）
    C.大众朗逸（4600mm×1700mm×1400mm）
    D.奥迪A4（4700mm×1800mm×1400mm）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）如图（1），已知：在△ABC中，∠BAC＝90°，AB=AC，直线m经过点A，BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.

    （2） 如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=,其中为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

    （3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合）,点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形，连接BD、CE,若∠BDA=∠AEC=∠BAC，试判断△DEF的形状.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们知道不等式的两边加（或减）同一个数（或式子），不等号的方向不变．不等式组是否也具有类似的性质呢？请解答下列问题．

    （1）完成下列填空：

    已知

    用“＜”或“＞”填空

    5+2_____3+1

    ﹣3﹣1_____﹣5﹣2

    1﹣2_____4+1

    （2）一般地，如果那么a+c_____b+d（用“＜”或“＞”填空）．请你说明上述性质的正确性．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】直线经过原点和点，点的坐标为.

    (1)求直线所对应的函数解析式;

    （2）当P在线段OA上时，设点横坐标为，三角形的面积为，写出关于的函数解析式，并指出自变量的取值范围；

    （3）当P在射线OA上时，在坐标轴上有一点,使（正整数），请直接写出点的坐标（本小题只要写出结果，不需要写出解题过程）

    查看答案和解析>>

    同步练习册答案