
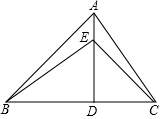
 如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.
如图,锐角△ABC中,∠ABC=45°,AD是高,E为AD上一点,BE=AC.分析 (1)在Rt△BDE和Rt△ADC中,根据HL证明全等即可.
(2)利用全等三角形的性质即可解决问题;
解答  (1)证明:∵AD是△ABC的高,
(1)证明:∵AD是△ABC的高,
∴∠BDE=∠ADC=90°,
∵∠ABC=45°,
∴∠DBA=∠DAB=45°,
∴BD=AD,
在Rt△BDE和Rt△ADC中,
$\left\{\begin{array}{l}{BD=AD}\\{BE=AC}\end{array}\right.$,
∴Rt△BDE≌Rt△ADC,
∴DE=DC.
(2)解:∵∠BAC=70°,∠DAB=45°,
∴∠DAC=25°,
∵△BDE≌△ADC,
∴∠DBE=∠DAC=25°,
∴∠ABE=∠ABD-∠DBE=45°-25°=20°.
点评 本题考查等腰直角三角形的判定和性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
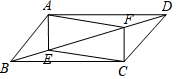 如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.
如图,在平行四边形ABCD中,E、F为对角线BD上两点,BE=DF,连接AE、EC、CF、FA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
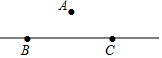 如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)
如图,高速公路BC(公路视为直线)的最高限速为120km/h,在该公路正上方离地面20m的点A处设置了一个测速仪,已知在点A测得点B的俯角为45°,点C的俯角为30°,测速仪监测到一辆汽车从点B匀速行驶到点C所用的时间是1.5s,试通过计算,判决该汽车在这段限速路上是否超速.(参考数据:$\sqrt{3}$≈1.7)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com