
【题目】如图,在长方形![]() 中,
中,![]() ,
,![]() ,动点
,动点![]() 、
、![]() 分别从点
分别从点![]() 、
、![]() 同时出发,点
同时出发,点![]() 以2厘米/秒的速度向终点
以2厘米/秒的速度向终点![]() 移动,点
移动,点![]() 以1厘米/秒的速度向
以1厘米/秒的速度向![]() 移动,当有一点到达终点时,另一点也停止运动.设运动的时间为
移动,当有一点到达终点时,另一点也停止运动.设运动的时间为![]() ,问:
,问:
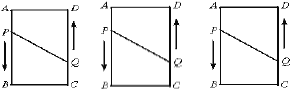
(1)当![]() 秒时,四边形
秒时,四边形![]() 面积是多少?
面积是多少?
(2)当![]() 为何值时,点
为何值时,点![]() 和点
和点![]() 距离是
距离是![]() ?
?
(3)当![]() _________时,以点
_________时,以点![]() 、
、![]() 、
、![]() 为顶点的三角形是等腰三角形.(直接写出答案)
为顶点的三角形是等腰三角形.(直接写出答案)
【答案】(1)5厘米2;(2)![]() 秒或
秒或![]() 秒;(3)
秒;(3)![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
试题(1)求出BP,CQ的长,即可求得四边形BCQP面积.
(2)过Q点作QH⊥AB于点H,应用勾股定理列方程求解即可.
(3)分PD=DQ,PD=PQ,DQ=PQ三种情况讨论即可.
(1)当t=1秒时,BP=6-2t=4,CQ=t=1,
∴四边形BCQP面积是![]() 厘米2.
厘米2.
(2)如图,过Q点作QH⊥AB于点H,则PH=BP-CQ=6-3t,HQ=2,
根据勾股定理,得![]() , 解得
, 解得![]() .
.
∴当![]() 秒或
秒或![]() 秒时,点P和点Q距离是3cm.
秒时,点P和点Q距离是3cm.
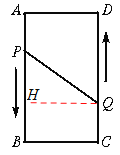
(3)∵![]() ,
,
当PD=DQ时,![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
当PD=PQ时,![]() ,解得
,解得![]() 或
或![]() (舍去);
(舍去);
当DQ=PQ时,![]() ,解得
,解得![]() 或
或![]() .
.
综上所述,当![]() 秒或
秒或![]() 秒或
秒或![]() 秒或
秒或![]() 秒时, 以点P、Q、D为顶点的三角形是等腰三角形.
秒时, 以点P、Q、D为顶点的三角形是等腰三角形.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形OABC中,点A的坐标是(﹣3,1),点B的纵坐标是4,则B,C两点的坐标分别是( )
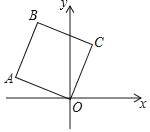
A. (﹣2,4),(1,3) B. (﹣2,4),(2,3)
C. (﹣3,4),(1,4) D. (﹣3,4),(1,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ABC=60°,AB=2.过点A作对角线BD的平行线与边CD的延长线相交于点E.P为边BD上的一个动点(不与端点B,D重合),连接PA,PE,AC.
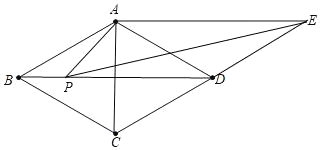
(1)求证:四边形ABDE是平行四边形;
(2)求四边形ABDE的周长和面积;
(3)记△ABP的周长和面积分别为C1和S1,△PDE的周长和面积分别为C2和S2,在点P的运动过程中,试探究下列两个式子的值或范围:①C1+C2,②S1+S2,如果是定值的,请直接写出这个定值;如果不是定值的,请直接写出它的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=![]() .其中正确的是( )
.其中正确的是( )
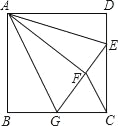
A. ①③ B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?
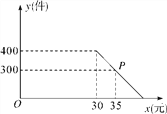
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校组织学生去某景点游玩,甲旅行社说:“如果带队的一名老师购买全票,则学生享受半价优惠”; 乙旅行社说:“所有人按全票价的六折优惠”.已知全票价为a元,学生有x人,带队老师有1人.
(1)试用含a和x的式子表示甲、乙旅行社的收费;
(2)若有30名学生参加本次活动,请你为他们选择一家更优惠的旅行社.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)8+(―![]() )―(―0.25)
)―(―0.25)
(2)-63÷7+45÷(-9)
(3)(-3)×(-9)-8×(-5)
(4)(-0.1)3-![]()
(5)-23-3×(-2)3-(-1)4
(6)(-![]()
(7)[11×2-|3÷3|-(-3)2-33]÷![]()
(8)2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动5个单位长度,从图中可以看出,终点表示的数是﹣2,已知A,B是数轴上的点.请参照图并思考,完成下列填空:
(1)如果点A表示数3,将点A向右移动7个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(2)如果点B表示数2,将点B向左移动9个单位长度,再向右移动5个单位长度,那么终点A表示的数是 ,A,B两点间的距离是 .

(3)如果点A表示的数是﹣4,将点A向右移动168个单位长度;再向左移动2个单位长度,那么终点B表示的数是 ,A,B两点间的距离是 .
(4)一般地,如果A点表示的数为m,将A点向右移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是 ,A,B两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com