
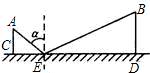
 如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是
如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是

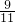

科目:初中数学 来源: 题型:
| 7 | 2 |
查看答案和解析>>
科目:初中数学 来源:中考备考专家数学(第二版) 题型:044
如图所示,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图.横断面的地平线为x轴,横断面的对称轴为y轴,桥拱的![]() 部分为一段抛物线,顶点G的高度为8米,AD和
部分为一段抛物线,顶点G的高度为8米,AD和![]() 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和![]() 为两个方向的汽车通行区,宽都为15米,线段CD和
为两个方向的汽车通行区,宽都为15米,线段CD和![]() 为两段对称的上桥斜坡,其坡度为1∶4.
为两段对称的上桥斜坡,其坡度为1∶4.
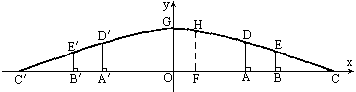
(1)求桥拱![]() 所在抛物线的解析式及
所在抛物线的解析式及![]() 的长.
的长.
(2)BE和![]() 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和![]() 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和![]() 的宽.
的宽.
(3)按规定,汽车通过该桥下时,载货最高处和桥拱之间的距离不得小于0.4米.今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离均为7米.它能否从OA(或![]() )区域安全通过?请说明理由.
)区域安全通过?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:044
如图所示,这是某市一处十字路口立交桥的横断面在平面直角坐标系中的示意图,横断面的地平线为x轴,横断面的对称轴为y轴,桥拱的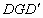 部分为一段抛物线,顶点G的高度为8米,AD和
部分为一段抛物线,顶点G的高度为8米,AD和 是两侧高为5.5米的支柱,OA和
是两侧高为5.5米的支柱,OA和 为两个方向的汽车通行区,宽都为15米,线段CD和
为两个方向的汽车通行区,宽都为15米,线段CD和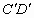 为两段对称的上桥斜坡,其坡度1:4.
为两段对称的上桥斜坡,其坡度1:4.
(1)求桥拱 所在抛物线的关系式及
所在抛物线的关系式及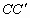 的长;
的长;
(2)BE和 为支撑斜坡的立柱,其高都为4米,相应的AB和
为支撑斜坡的立柱,其高都为4米,相应的AB和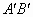 为两个方向的行人及非机动车通行区,试求AB和
为两个方向的行人及非机动车通行区,试求AB和 的宽;
的宽;
(3)按规定,汽车能过该桥下时,载货最高处和桥拱之间的距离不能小于0.4米,今有一大型运货汽车,装载某大型设备后,其宽为4米,车载大型设备的顶部与地面的距离为7米,它能否从OA(和 )区域安全通过?请说明理由.
)区域安全通过?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2010年广西贺州市中考数学试卷(解析版) 题型:解答题
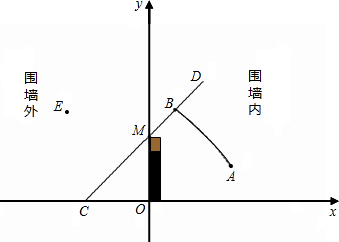
 ),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)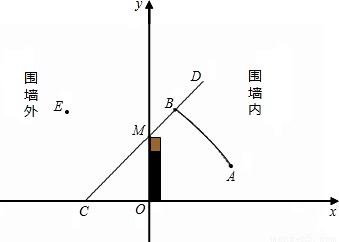
查看答案和解析>>
科目:初中数学 来源:2011年广西河池市宜州市中考数学一模试卷(解析版) 题型:解答题
 ),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
),点B和点E关于此二次函数图象的对称轴对称,若tan∠OCM=1.(围墙的厚度忽略不计,围墙内外水平面高度一样)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com