
| A. | ①② | B. | ①②④ | C. | ①②⑤ | D. | ①②④⑤ |
分析 ①根据二次函数图象与x轴有两个不同的交点,结合根的判别式即可得出△=b2-4ac>0,①正确;②由点M(x0,y0)在二次函数图象上,利用二次函数图象上点的坐标特征即可得出x=x0是方程ax2+bx+c=y0的解,②正确;③分a>0和a<0考虑,当a>0时得出x1<x0<x2;当a<0时得出x0<x1或x0>x2,③错误;④将二次函数的解析式由一般式转化为交点式,再由点M(x0,y0)在x轴下方即可得出y0=a(x0-x1)(x0-x2)<0,④正确;⑤根据③可得出⑤错误.综上即可得出结论.
解答 解:①∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),且x1<x2,
∴方程ax2+bx+c=0有两个不相等的实数根,
∴△=b2-4ac>0,①正确;
②∵图象上有一点M(x0,y0),
∴a${{x}_{0}}^{2}$+bx0+c=y0,
∴x=x0是方程ax2+bx+c=y0的解,②正确;
③当a>0时,∵M(x0,y0)在x轴下方,
∴x1<x0<x2;
当a<0时,∵M(x0,y0)在x轴下方,
∴x0<x1或x0>x2,③错误;
④∵二次函数y=ax2+bx+c(a≠0)的图象于x轴的交点坐标分别为(x1,0),(x2,0),
∴y=ax2+bx+c=a(x-x1)(x-x2),
∵图象上有一点M(x0,y0)在x轴下方,
∴y0=a(x0-x1)(x0-x2)<0,④正确;
⑤根据③即可得出⑤错误.
综上可知正确的结论有①②④.
故选B.
点评 本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征以及二次函数图象与系数的关系,根据二次函数的相关知识逐一分析五条结论的正误是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
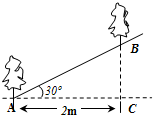 如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB为( )m.
如图,沿倾斜角为30°的山坡植树,要求相邻两棵树间的水平距离AC为2m,那么相邻两棵树的斜坡距离AB为( )m.| A. | $\frac{4}{3}$$\sqrt{3}$ | B. | $\frac{2}{3}$$\sqrt{3}$ | C. | 1 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
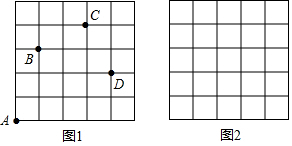
 如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其他甲虫.规定:向上、向右走为正,向下、向左走为负.如从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中
如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其他甲虫.规定:向上、向右走为正,向下、向左走为负.如从A到B记为:A→B(+1,+4),从B到A记为:A→B(-1,-4),括号内第一个数表示左右方向,第二个数表示上下方向,那么图中查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com