练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知A=2x2﹣9x﹣11，B=3x2﹣6x+4．求：
    （1）A﹣B；
    （2）A+2B．

    【答案】
    （1）

    解：∵A=2x2﹣9x﹣11，B=3x2﹣6x+4，

    ∴A﹣B

    =2x2﹣9x﹣11﹣3x2+6x﹣4

    =﹣x2﹣3x﹣15


    （2）

    解：∵A=2x2﹣9x﹣11，B=3x2﹣6x+4，

    ∴

    = （2x2﹣9x﹣11）+2（3x2﹣6x+4）

    =x2﹣4.5x﹣5.5+6x2﹣12x+8

    =7x2﹣16.5x+2.5


    【解析】（1）根据A=2x2﹣9x﹣11，B=3x2﹣6x+4，可以求得A﹣B的值；（2）根据A=2x2﹣9x﹣11，B=3x2﹣6x+4，可以求得 A+2B的值．
    【考点精析】本题主要考查了整式加减法则的相关知识点，需要掌握整式的运算法则：（1）去括号；（2）合并同类项才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，EF∥AD，∠1=∠2，将求证AB∥DG的过程填空完整．
    证明：∵EF∥AD（________）
    ∴∠2=________（________）
    又∵∠1=∠2（________）
    ∴∠1=∠3（________）
    ∴AB∥________（________）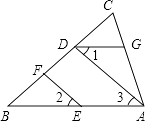

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一元二次方程x2+x﹣6=0的根的情况是（ ）
    A.有两个相等的实根
    B.没有实数根
    C.有两个不相等的实根
    D.无法确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校九年级上学期期中考试后从全年级400名学生中抽取了60名学生的考试成绩作为一个样本，用来分析全年级的考试成绩情况，这个问题的样本容量是____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC．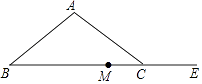
    （1）尺规作图：作∠ABC的平分线，交AC于点D（保留作图痕迹，不写作法）；
    （2）E是底边BC的延长线上一点，M是BE的中点，连接DE、DM．若CE=CD，求证：DM⊥BE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点E在AC的延长线上，下列条件中能判断AB∥CD的是（ ）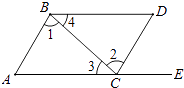

    A.∠3=∠4
    B.∠D=∠DCE
    C.∠1=∠2
    D.∠D+∠ACD=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义运算 = ，若a≠﹣1，b≠﹣1，则下列等式中不正确的是（ ）
    A. × =1
    B. + =
    C.（ ）2=
    D. =1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ACB中，∠ACB=90゜，CD⊥AB于D．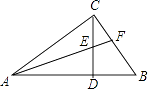

    （1）求证：∠ACD=∠B；
    （2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF=∠CFE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】钝角三角形ABC中，∠BAC＞90°，∠ACB=α，∠ABC=β，过点A的直线l交BC边于点D．点E在直线l上，且BC=BE．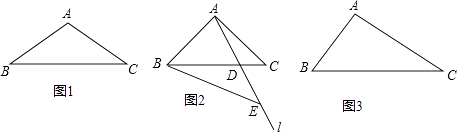

    （1）若AB=AC，点E在AD延长线上．
    当α=30°，点D恰好为BE中点时，补全图1，直接写出∠BAE=°，
    ∠BEA=°；
    （2）如图2，若∠BAE=2α，求∠BEA的度数（用含α的代数式表示）；
    （3）如图3，若AB＜AC，∠BEA的度数与（1）中②的结论相同，直接写出∠BAE，α，β满足的数量关系．

    查看答案和解析>>

    同步练习册答案