
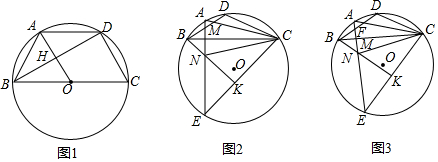
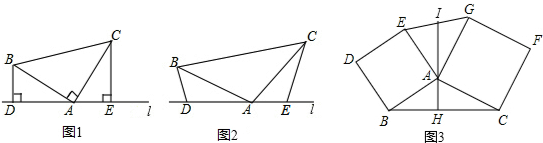
分析 (1)如图1,连接OD,分别证明四边形AOCD和四边形ABOD是平行四边形,得AH=OH,再根据OH是△BDC的中位线,得DC=2OH,所以DC=2AH;
(2)如图2,连接AB,根据三角形的内角和求得∠NBM=∠KEN,证明△ABM≌△NBM,再证明BC是AN的中垂线,可以得出结论;
(3)如图3,作辅助线构建直角三角形,证明DE⊥AC得CD=CG=17,MG=BM=4,BC=25,在△BCH中分别求CH和BH的长,可得BD=BH-DH,代入可得结论.
解答 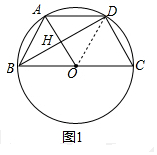 证明:(1)如图1,连接OD,
证明:(1)如图1,连接OD,
∵点A为弧$\widehat{BD}$的中点,
∴OA⊥BD,
∴∠BHO=90°,BH=HD,
∵BC是⊙O的直径,
∴∠BDC=90°,
∴∠BDC=∠BHO,
∴AO∥DC,
∵AD∥BC,
∴四边形AOCD是平行四边形,
∴AD=OC=BO,
∴四边形ABOD是平行四边形,
∴AH=HO,
∵BH=HD,BO=OC,
∴OH为△BDC的中位线,
∴DC=2OH,
∴DC=2AH;
(2)如图2,连接AB,
∵AE⊥BC,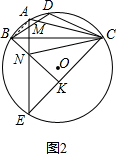
∴∠BMN=90°,
∵BK⊥EC,
∴∠EKN=90°,
∴∠BMN=∠EKN,
∵∠BNM=∠ENK,
∴∠NBM=∠KEN,
∵∠ABC=∠KEN,
∴∠NBM=∠ABC,
∵BM=BM,∠AMB=∠BMN=90°,
∴△ABM≌△NBM,
∴AM=MN,
∴BC是AN的中垂线,
∴AC=NC,
∴∠CAN=∠CNA;
(3)如图3,过C作CH⊥BD,交BD的延长线于H,连接BE、DE,DE交BC于G,交AC于P,
∵点A为弧$\widehat{BD}$的中点,
∴$\widehat{AB}$=$\widehat{AD}$,
∴∠DCA=∠ACB,∠AEB=∠AED,
∵∠BME=∠GME=90°,EM=EM,
∴△BME≌△GME,
∴BM=MG,∠EBC=∠EGB,
∵∠EDC=∠EBC,∠EGB=∠DGC,
∴∠EDC=∠DGC,
∴△DGC是等腰三角形,
∴AC⊥DE,CG=CD=17,
∵tan∠DBC=$\frac{3}{4}$=$\frac{FM}{BM}$,
设FM=3x,BM=4x,则BF=5x,
∵BF=5,
∴FM=3,BM=4,
∴BC=BM+MG+CG=4+4+17=25,
在Rt△BHC中,tan∠DBC=$\frac{CH}{BH}=\frac{3}{4}$,
设CH=3a,BH=4a,则BC=5a,
5a=25,a=5,
∴CH=3a=3×5=15,BH=4a=4×5=20,
由勾股定理得:DH=$\sqrt{D{C}^{2}-C{H}^{2}}$=$\sqrt{1{7}^{2}-1{5}^{2}}$=8,
∴BD=BH-DH=20-8=12.
点评 本题是圆的综合题,难度较大,考查了圆周角定理、垂径定理、相似三角形的性质与判定以及三角函数,本题的关键是作辅助线构建直角三角形和等腰三角形,以求出BC的长这突破口,依次根据三角函数列比例式或设未知数求边的长度.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:填空题
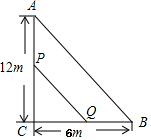 如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?
如图,在Rt△ABC中,∠C=90°,点P、Q同时由C、B两点出发,点P在CA上沿CA方向以2cm/s的速度移动,点Q在BC上沿BC方向以1cm/s的速度移动,则2或4秒钟后,△PCQ的面积为8cm2?查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com