
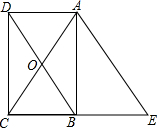
 如图,矩形ABCD的对角线AC、BD相交于点O.过点A作AE∥BD,交CB的延长线于点E.
如图,矩形ABCD的对角线AC、BD相交于点O.过点A作AE∥BD,交CB的延长线于点E.分析 (1)由矩形的性质,可得AC=BD,欲求AC=AE,证BD=AE即可.可通过证四边形AEBD是平行四边形,从而得出AC=AE的结论;
(2)只要证明△OBC是等边三角形,即可解决问题;
解答 解:(1)证明:在矩形ABCD中,AC=BD,AD∥BC,
又∵AE∥BD,
∴四边形AEBD是平行四边形.
∴BD=AE,
∴AC=AE;
(2)∵∠AOB=120°,
∴∠BOC=60°,
∵四边形ABCD是矩形,
∴OB=OC,
∴△OBC是等边三角形,
∴BC=OC=$\frac{1}{2}$AC=$\frac{1}{2}$AE=4.
点评 本题考查了矩形的性质,平行四边形的判定和性质、等边三角形的判定和性质等知识,了解矩形的特殊性质是解答本题的关键,本题难度不大,但综合性较强.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;
(1)计算:|$\sqrt{2}$-$\sqrt{3}$|+2$\sqrt{2}$;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).
如图,是利用平面直角坐标系画出的天安门广场的平面示意图,若这个坐标系分别以正东、正北方向为x轴、y轴的正方向,表示毛主席纪念堂的点的坐标为(0,-3),表示中国国家博物馆的点的坐标为(4,1),则表示人民大会堂的点的坐标为(-4,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com