
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB交弧BC于点D,AD与OC交于点E,连接CD、OD,给出以下四个结论: ①AC∥OD;②CE=OE;③∠CDE=∠COD;④2CD2=CEAB.
其中正确结论的序号是(在横线上填上你认为所有正确结论的代号).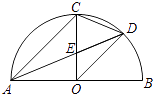
【答案】①③④
【解析】解:∵AB是半圆直径, ∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO= ![]() ∠CAB,
∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,故①正确.
由题意得,OD=R,AC= ![]() R,
R,
∵OE:CE=OD:AC= ![]() ,
,
∴OE≠CE,故②错误;
∵AB是半圆直径,半径OC⊥AB于点O,
∴∠AOC=∠COB=90°,
∴∠CDE= ![]() ∠AOC=45°,
∠AOC=45°,
∵OA=OC,
∴∠CAO=45°,
∵AD平分∠CAB交弧BC于点D,
∴∠DAO=22.5°,
∴∠COD=2∠CAD=45°,
∴∠CDE=∠COD;故③正确;
∵AD平分∠CAB交弧BC于点D,
∴∠CAD= ![]() ×45°=22.5°,
×45°=22.5°,
∴∠COD=45°,
∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°
∵∠CAD=∠ADO=22.5°(已证),
∴∠CDE=∠ODC﹣∠ADO=67.5°﹣22.5°=45°,
∴△CED∽△CDO,
∴ ![]() ,
,
∴CD2=COCE= ![]() ABCE,
ABCE,
∴2CD2=CEAB,故④正确.
综上可得①③④正确.
所以答案是:①③④,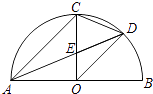
【考点精析】通过灵活运用圆周角定理和相似三角形的判定与性质,掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于点E,垂足为F,连接CD,BE
(1)求证:CE=AD
(2)若D为AB的中点,则∠A的度数满足什么条件时,四边形BECD是正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,BE⊥AC于点E,AD⊥BC于点D,
∠BAD=45°,AD与BE交于点F,连接CF.
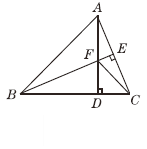
(1)求证:BF=2AE;
(2)若CD=![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是矩形ABCD内的一个动点,连接EA、EB、EC、ED,得到△EAB、△EBC、△ECD、△EDA,设它们的面积分别是m、n、p、q,给出如下结论:
①m+n=q+p;
②m+p=n+q;
③若m=n,则E点一定是AC与BD的交点;
④若m=n,则E点一定在BD上.
其中正确结论的序号是( )

A. ①③ B. ②④ C. ①②③ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
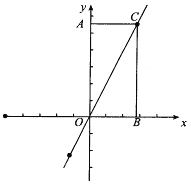
【题目】有一长方形AOBC纸片放在如图所示的坐标系中,且长方形的两边的比为OA:AC=2:1.
(1)求直线OC的解析式;
(2)求出![]() =-5时,函数
=-5时,函数![]() 的值;
的值;
(3)求出![]() =-5时,自变量
=-5时,自变量![]() 的值;
的值;
(4)画这个函数的图象;
(5)根据图象回答,当![]() 从2减小到-3时,
从2减小到-3时,![]() 的值是如何变化的?
的值是如何变化的?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com