
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 当m=0时,二次函数图象的顶点坐标为(0,0) | |
| B. | 当m<0时,二次函数图象的对称轴在y轴右侧 | |
| C. | 若将该函数图象沿y轴向下平移6个单位,则平移后图象与x轴两交点之间的距离为$2\sqrt{3}$ | |
| D. | 设二次函数的图象与y轴交点为A,过A作x轴的平行线,交图象于另一点B,抛物线的顶点为C,则△ABC的面积为m3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )
甲、乙两车从A城出发前往B城,在整个行驶过程中,汽车离开A城的距离y(km)与行驶时间t(h)的函数图象如图所示,下列说法正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要消去y,可以将①×5+②×2 | B. | 要消去x,可以将①×3+②×(-5) | ||
| C. | 要消去y,可以将①×5+②×3 | D. | 要消去x,可以将①×(-5)+②×2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
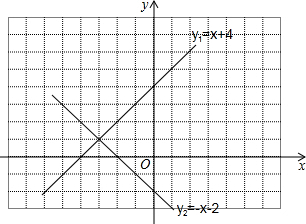 在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答:
在同一平面直角坐标系内画直线y1=x+4和y2=-x-2图象,根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
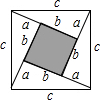 如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.
如图正方形的面积可以用两种方法得出:即c2或(b-a)2+4×$\frac{1}{2}ab$,由此可推出a2+b2=c2,若直角三角形中两直角边的和a+b=4,斜边c长为3,利用该等式来计算直角三角形的面积是$\frac{7}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com