
【题目】在北京市开展的“首都少年先锋岗”活动中,某数学小组到人民英雄纪念碑站岗执勤,并在活动后实地测量了纪念碑的高度. 方法如下:如图,首先在测量点A处用高为1.5m的测角仪AC测得人民英雄纪念碑MN顶部M的仰角为35°,然后在测量点B处用同样的测角仪BD测得人民英雄纪念碑MN顶部M的仰角为45°,最后测量出A,B两点间的距离为15m,并且N,B,A三点在一条直线上,连接CD并延长交MN于点E. 请你利用他们的测量结果,计算人民英雄纪念碑MN的高度.
(参考数据:sin35°≈0.6,cos35°≈0.8,tan35°≈0.7)

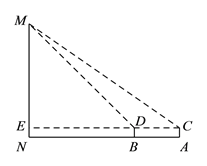
【答案】人民英雄纪念碑MN.的高度约为36.5米.
【解析】试题分析:由题意得,四边形ACDB,ACEN为矩形,从而得EN=AC=1.5.AB=CD=15,在Rt△MED中,由题意可得ME=DE,设ME=DE=x,则EC=x+15,在Rt△MEC中,可得ME=ECtan∠MCE,从而有x≈0.7(x+15),求出x的值,从而得MN=ME+EN≈36.5 .
试题解析:由题意得,四边形ACDB,ACEN为矩形,
∴EN=AC=1.5,AB=CD=15,
在![]() 中,
中,
∠MED=90°,∠MDE=45°,
∴∠EMD=∠MDE=45°,
∴ME=DE,
设ME=DE=x,则EC=x+15,
在![]() 中,∠MEC=90°,
中,∠MEC=90°,
∠MCE=35°,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴人民英雄纪念碑MN.的高度约为36.5米.


 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案科目:初中数学 来源: 题型:
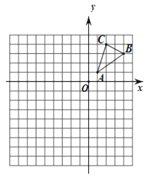
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
(1)请作出![]() 绕
绕![]() 点逆时针旋转
点逆时针旋转![]() 的
的![]() ;
;
(2)以点![]() 为位似中心,将
为位似中心,将![]() 扩大为原来的2倍,得到
扩大为原来的2倍,得到![]() ,请在
,请在![]() 轴的左侧画出
轴的左侧画出![]() ;
;
(3)请直接写出![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
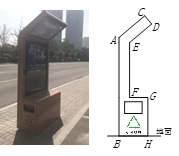
【题目】在太原迎泽西大街上有一种智能垃圾桶,这种智能垃圾桶不仅可以供行人休息,灯箱边的中部还有USB接口可供行人充电.此种垃圾桶的侧面示意图如图所示,其中AC∥ED,AB∥EF∥GH,CD=20cm,DE=60cm,EF=100m,GH=80cm,∠CDE=∠EFG=90°,∠DEF=130°,则此种垃圾桶的高度(C到地面的距离)约为________cm.(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c的对称轴为直线x=﹣1,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b<0;其中正确的个数有( )
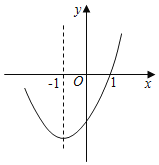
A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在全国初中数学联赛中,将参赛两个班学生的成绩(得分均为整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图所示),已知图中从左到右的第一、第三、第四、第五小组的频率分别是0.25、0.15、0.10、0.10,第二组的频数是40.
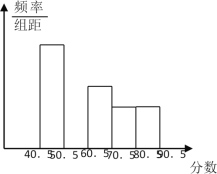
(1)第二小组的频率是_____,并补全这个频率分布直方图;
(2)这两个班参赛的学生人数是_________;
(3)这两个班参赛学生的成绩的中位数落在第______组内.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们定义:如图1,在△ABC看,把AB点绕点A顺时针旋转α(0°<α<180°)得到AB',把AC绕点A逆时针旋转β得到AC',连接B'C'.当α+β=180°时,我们称△A'B'C'是△ABC的“旋补三角形”,△AB'C'边B'C'上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.
特例感知:
(1)在图2,图3中,△AB'C'是△ABC的“旋补三角形”,AD是△ABC的“旋补中线”.
①如图2,当△ABC为等边三角形时,AD与BC的数量关系为AD= BC;
②如图3,当∠BAC=90°,BC=8时,则AD长为 .
猜想论证:
(2)在图1中,当△ABC为任意三角形时,猜想AD与BC的数量关系,并给予证明.
拓展应用
(3)如图4,在四边形ABCD,∠C=90°,∠D=150°,BC=12,CD=2![]() ,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.
,DA=6.在四边形内部是否存在点P,使△PDC是△PAB的“旋补三角形”?若存在,给予证明,并求△PAB的“旋补中线”长;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】唐山世园会期间,游乐场投资150万元引进一项大型游乐设施.若不计维修保养费用,预计开放后每月可创收31万元.而该游乐场开放后,从第1个月到第x个月的维修保养费用累计为y(万元),且y=ax2+bx.若将创收扣除投资和维修保养费用称为游乐场的纯收益g(万元),g也是关于x的二次函数.
(1)若维修保养费用第1个月为2万元,第2个月为4万元,求y关于x的解析式;
(2)求纯收益g关于x的解析式;
(3)问设施开放几个月后,游乐场的纯收益达到最大?并求出最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com