
【题目】如图,等腰直角三角形ABC,∠BAC=90°,D、E是BC上的两点,且BD=CE,过D、E作DM、EN分别垂直AB、AC,垂足为M、N,交与点F,连接AD、AE.其中①四边形AMFN是正方形;②△ABE≌△ACD;③CE2+BD2=DE2;④当∠DAE=45°时,AD2=DECD.正确结论有( )
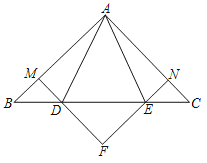
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由三个角是直角的四边形是矩形,先判定四边形AMFN是矩形,再证明AM=AN,从而可判断①;利用SAS可判定△ABE≌△ACD,从而可判断②;在没有∠DAE=45°时,无法证得DE′=DE,故可判断③;由∠DAE=∠C,∠ADE=∠CDA可判定△ADE∽△CDA,从而可判定④.
解:∵DM、EN分别垂直AB、AC,垂足为M、N,
∴∠AMF=∠ANF=90°,
又∵∠BAC=90°,
∴四边形AMFN是矩形;
∵△ABC为等腰直角三角形,
∴AB=AC,∠ABC=∠C=45°,
∵DM⊥AB,EN⊥AC,
∴△BDM和△CEN均为等腰直角三角形,
又∵BD=CE,
∴△BDM≌△CEN(AAS),
∴BM=CN
∴AM=AN,
∴四边形AMFN是正方形,故①正确;
∵BD=CE,
∴BE=CD,
∵△ABC为等腰直角三角形,
∴∠ABC=∠C=45°,AB=AC,
∴△ABE≌△ACD(SAS),故②正确;
如图所示,将△ACE绕点A顺时针旋转90°至△ABE′,则CE=BE′,∠E′BA=∠C=45°,
由于△BDM≌△CEN,故点N落在点M处,连接ME′,则D、M、E′共线,
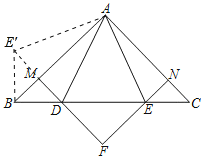
∵∠E′BA=45°,∠ABC=45°,
∴∠DBE′=90°,
∴BE′2+BD2=DE′2,
∴CE2+BD2=DE′2,
当∠DAE=45°时,∠DAE′=∠DAM+∠EAN=90°﹣45°=45°,
AE=AE′,AD=AD,
∴△ADE≌△ADE′(SAS),
∴DE′=DE,
∴在没有∠DAE=45°时,无法证得DE′=DE,故③错误;
∵AB=AC,∠ABD=∠C,BD=CE,
∴△ABD≌△ACE(SAS),
∴AD=AE,
∴当∠DAE=45°时,∠ADE=∠AED=67.5°,
∵∠C=45°,
∴∠DAE=∠C,∠ADE=∠CDA,
∴△ADE∽△CDA,
∴![]() =
=![]() ,
,
∴AD2=DECD,故④正确.
综上,正确的有①②④,共3个.
故选:C.


科目:初中数学 来源: 题型:
【题目】某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
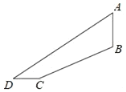
A.5.6B.6.9C.11.4D.13.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆快递车从长春出发,走高速公路,途经伊通,前往靖宇镇送快递,到达后卸货和休息共用1h,然后开车按原速原路返回长春.这辆快递车在长春到伊通、伊通到靖宇的路段上分别保持匀速前进,这辆快递车距离长春的路程y(km)与它行驶的时间x(h)之间的函数图象如图所示.
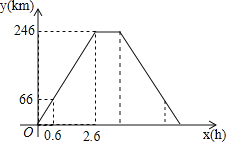
(1)快递车从伊通到长春的速度是______km/h,往返长春和靖宇两地一共用时______h.
(2)当这辆快递车在靖宇到伊通的路段上行驶时,求y与x之间的函数关系式,并写出自变量x的取值范围.
(3)如果这辆快递车两次经过同一个服务区的时间间隔为4h,直接写出这个服务区距离伊通的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进![]() 、
、![]() 两种商品,购买1个
两种商品,购买1个![]() 商品比购买1个
商品比购买1个![]() 商品多花10元,并且花费300元购买
商品多花10元,并且花费300元购买![]() 商品和花费100元购买
商品和花费100元购买![]() 商品的数量相等.
商品的数量相等.
(1)求购买一个![]() 商品和一个
商品和一个![]() 商品各需要多少元;
商品各需要多少元;
(2)商店准备购买![]() 、
、![]() 两种商品共80个,若
两种商品共80个,若![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的4倍,并且购买
商品数量的4倍,并且购买![]() 、
、![]() 商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
商品的总费用不低于1000元且不高于1050元,那么商店有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |

(1)表中![]() __________;
__________;![]() _________.
_________.
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
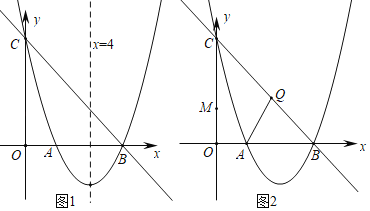
【题目】如图1所示,已知直线y=kx+m与抛物线y=ax2+bx+c分别交于x轴和y轴上同一点,交点分别是点B(6,0)和点C(0,6),且抛物线的对称轴为直线x=4;
(1)试确定抛物线的解析式;
(2)在抛物线的对称轴上是否存在点P,使△PBC是直角三角形?若存在请直接写出P点坐标,不存在请说明理由;
(3)如图2,点Q是线段BC上一点,且CQ=![]() ,点M是y轴上一个动点,求△AQM的最小周长.
,点M是y轴上一个动点,求△AQM的最小周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
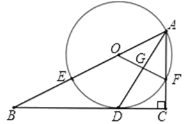
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)求证:![]() ;
;
(3)若BE=8,sinB=![]() ,求AD的长,
,求AD的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市体育中考现场考试内容有三项:50米跑为必测项目.另在立定跳远、实心球(二选一)和坐位体前屈、1分钟跳绳(二选一)中选择两项.
(1)每位考生有_________种选择方案;
(2)求小明与小刚选择同种方案的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:⊙O的两条弦AB,CD相交于点M,且AB=CD.
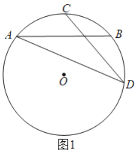
(1)如图1,连接AD.求证:AM=DM.
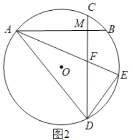
(2)如图2,若AB⊥CD,在弧BD上取一点E,使弧BE=弧BC,AE交CD于点F,连AD、DE.
①利断∠E与∠DFE是否相等,并说明理由.
②若DE=7,AM+MF=17,求△ADF的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com