
【题目】在全国预防“新冠肺炎”时期,某厂接受了生产一批高质量医用口罩的任务.要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产
型口罩不得少于1.8万只.该厂的生产能力是:每天只能生产一种型号的口罩,若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只.已知生产6只
型口罩每天能生产0.8万只.已知生产6只![]() 型和10只
型和10只![]() 型口罩一共获利6元,生产4只
型口罩一共获利6元,生产4只![]() 型和5只
型和5只![]() 型口罩一共获利3.5元
型口罩一共获利3.5元
(1)生产一只![]() 型口罩和
型口罩和![]() 型口罩分别获利多少钱?
型口罩分别获利多少钱?
(2)若生产![]() 型口罩
型口罩![]() 万只,该厂这次生产口罩的总利润为
万只,该厂这次生产口罩的总利润为![]() 万元,请求出
万元,请求出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)在完成任务的前提下,如何安排生产![]() 型和
型和![]() 型口罩的只数,使获得的总利润最大?最大利润是多少?
型口罩的只数,使获得的总利润最大?最大利润是多少?
【答案】(1)每只![]() 型口罩销售利润为0.2元,每只
型口罩销售利润为0.2元,每只![]() 型口罩销售利润为0.3元;(2)表达式为
型口罩销售利润为0.3元;(2)表达式为![]() ;(3)在完成任务的前提下,生产
;(3)在完成任务的前提下,生产![]() 型和
型和![]() 型口罩的只数分别为1.8万和3.2万可以使获得的总利润最大,最大利润是13200元.
型口罩的只数分别为1.8万和3.2万可以使获得的总利润最大,最大利润是13200元.
【解析】
(1)设每只![]() 型口罩销售利润为
型口罩销售利润为![]() 元,每只
元,每只![]() 型口罩销售利润为
型口罩销售利润为![]() 元,根据题意得
元,根据题意得
![]() ,解方程组即可得到答案;
,解方程组即可得到答案;
(2)根据总利润=A的生产数量乘以A的利润+B的生产数量乘以B的利润,要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只,得
型口罩不得少于1.8万只,得![]() ,又由生产力有限且8天之内要完成5万个口罩,假设最多用t天生产A型,求得x的最大值,即可得到x的取值范围是
,又由生产力有限且8天之内要完成5万个口罩,假设最多用t天生产A型,求得x的最大值,即可得到x的取值范围是![]() ,从而得到答案;
,从而得到答案;
(3)由题意“若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只”且“每只
型口罩每天能生产0.8万只”且“每只![]() 型口罩销售利润为0.2元,每只
型口罩销售利润为0.2元,每只![]() 型口罩销售利润为0.3元”可知多生产B型口罩能获取更多利润且生产速度也比A的要快,故尽量多生产B比较有利,故得到A型生产、B型生产数量.将A=1.8万代入
型口罩销售利润为0.3元”可知多生产B型口罩能获取更多利润且生产速度也比A的要快,故尽量多生产B比较有利,故得到A型生产、B型生产数量.将A=1.8万代入![]() 计算得到答案.
计算得到答案.
解:(1)设每只![]() 型口罩销售利润为
型口罩销售利润为![]() 元,每只
元,每只![]() 型口罩销售利润为
型口罩销售利润为![]() 元,根据题意得
元,根据题意得
![]() 解得
解得![]() ,
,
答:每只![]() 型口罩销售利润为0.2元,每只
型口罩销售利润为0.2元,每只![]() 型口罩销售利润为0.3元;
型口罩销售利润为0.3元;
(2)根据总利润=A的生产数量乘以A的利润+B的生产数量乘以B的利润,要求8天之内(含8天)生产![]() 型和
型和![]() 型两种型号的口罩共5万只,其中
型两种型号的口罩共5万只,其中![]() 型口罩不得少于1.8万只,得
型口罩不得少于1.8万只,得![]() ,即
,即![]() ,又因为生产力有限且8天之内要完成5万个口罩,所以假设最多用t天生产A型,则(8-t)天生产B型,则依据题意可得
,又因为生产力有限且8天之内要完成5万个口罩,所以假设最多用t天生产A型,则(8-t)天生产B型,则依据题意可得![]() ,解得t=7,故x的最大值只能是
,解得t=7,故x的最大值只能是![]() ,故x的取值范围是
,故x的取值范围是![]() ,所以表达式为
,所以表达式为![]() ;
;
(3)由题意“若生产![]() 型口罩每天能生产0.6万只,若生产
型口罩每天能生产0.6万只,若生产![]() 型口罩每天能生产0.8万只”且“每只
型口罩每天能生产0.8万只”且“每只![]() 型口罩销售利润为0.2元,每只
型口罩销售利润为0.2元,每只![]() 型口罩销售利润为0.3元”可知多生产B型口罩能获取更多利润且生产速度也比A的要快,故尽量多生产B比较有利,所以A型生产1.8万,B型生产
型口罩销售利润为0.3元”可知多生产B型口罩能获取更多利润且生产速度也比A的要快,故尽量多生产B比较有利,所以A型生产1.8万,B型生产![]() 万.将A=1.8万代入
万.将A=1.8万代入![]() 得到
得到![]() .
.
答:在完成任务的前提下,生产![]() 型和
型和![]() 型口罩的只数分别为1.8万和3.2万可以使获得的总利润最大,最大利润是13200元.
型口罩的只数分别为1.8万和3.2万可以使获得的总利润最大,最大利润是13200元.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】2020年初,新冠肺炎肆虐全球.我国政府和人民采取了积极有效的防疫措施,疫情在我国得到了有效控制.小明为复学到药店购买![]() 口罩和一次性医用口罩.已知购买
口罩和一次性医用口罩.已知购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用口罩共需
个一次性医用口罩共需![]() 元;购买
元;购买![]() 个
个![]() 口罩和
口罩和![]() 个一次性医用罩共需
个一次性医用罩共需![]() 元.
元.
(1)求![]() 口罩与一次性医用口罩的单价;
口罩与一次性医用口罩的单价;
(2)小明准备购买![]() 口罩和一次性医用口罩共
口罩和一次性医用口罩共![]() 个,且
个,且![]() 口罩的数量不少于一次性医用口罩数量的
口罩的数量不少于一次性医用口罩数量的![]() .请设计出最省钱的购买方案,并说明理由.
.请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
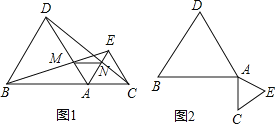
【题目】如图1,点A是线段BC上一点,△ABD,△AEC都是等边三角形,BE交AD于点M,CD交AE于N.
(1)求证:BE=DC;
(2)求证:△AMN是等边三角形;
(3)将△ACE绕点A按顺时针方向旋转90°,其它条件不变,在图2中补出符合要求的图形,并判断(1)、(2)两小题结论是否仍然成立,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
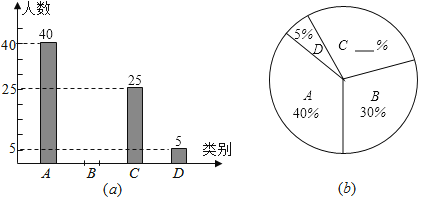
【题目】为了了解某区2018年初中毕业生毕业后的去向,某区教育部门对部分初三学生进行了抽样调查,就初三学生的四种去向(A,读普通高中;B,读职业高中;C,直接进入社会就业;D,其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问:
(1)此次共调查了多少名初中毕业生?
(2)将两幅统计图中不完整的部分补充完整;
(3)若某区2018年初三毕业生共有3500人,请估计2019年初三毕业生中读普通高中的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“低碳生活,绿色出行”是一种环保、健康的生活方式,小丽从甲地出发沿一条笔直的公路骑行前往乙地,她与乙地之间的距离y(km)与出发时间t(h)之间的函数关系如图中线段AB所示,在小丽出发的同时,小明从乙地沿同一条公路汽骑车匀速前往甲地,两人之间的距离s(km)与出发时间t(h)之间的函数关系如图中折线段AD-DE-EF所示,则E点坐标为
________.

查看答案和解析>>
科目:初中数学 来源: 题型:
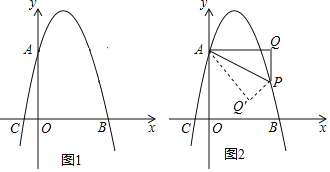
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,试过点P作x轴的垂线1,再过点A作1的垂线,垂足为Q,连接AP.
(1)求抛物线的函数表达式和点C的坐标;
(2)若△AQP∽△AOC,求点P的横坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧时,若将△APQ沿AP对折,点Q的对应点为点Q′,请直接写出当点Q′落在坐标轴上时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠A=30°,将△ABC绕C点按逆时针方向旋转![]() 角(0°<
角(0°<![]() <90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角
<90°)得到△DEC,设CD交AB于点F,连接AD,当旋转角![]() 度数为________,△ADF是等腰三角形.
度数为________,△ADF是等腰三角形.
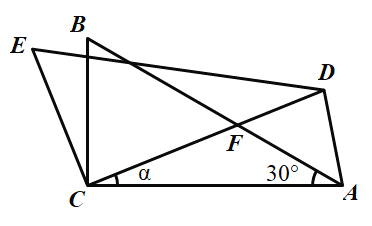
A.20°B.40°C.10°D.20°或40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com